
分析 (1)根据一元二次方程的定义和根的判别式得到k≠0且(k+2)2-4k•$\frac{k}{4}$>0,然后求出两个不等式的公共部分即可;
(2)假设存在实数k使方程的两个实数根的倒数和等于0,利用根与系数的关系得出x1+x2=-$\frac{k+2}{k}$,x1x2=$\frac{1}{4}$利用两个实数根的倒数和等于0,得出方程的解,结合k的取值范围判定即可.
解答 解:(1)∵关于x的方程kx2+(k+2)x+$\frac{k}{4}$=0有两个不相等的实数根,
∴k≠0且△>0,即(k+2)2-4k•$\frac{k}{4}$>0,
∴k>-1且k≠0.
(2)不存在.
理由:假设存在实数k使方程的两个实数根的倒数和等于0,
∵x1+x2=-$\frac{k+2}{k}$,x1x2=$\frac{1}{4}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{4(k+2)}{k}$=0,
解得:k=-2
∵k>-1,
∴不存在实数k使方程的两个实数根的倒数和等于0.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


科目:初中数学 来源: 题型:解答题
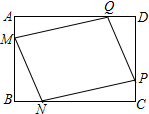 某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2
某小区在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化,为了绿化环境又节省成本.如图,已知矩形的边BC=200m,边AB=a m(a为不大于200的常数),四边形MNPQ的顶点在矩形的边上,且AM=BN=CP=DQ=x m,设四边形MNPQ的面积为S m2查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=A′B′,BC=B′C′,∠A=∠A′ | |
| B. | ∠A=∠A′,∠B=∠B′,AC=B′C′ | |
| C. | ∠A=∠A′,∠B=∠B′,∠C=∠C′ | |
| D. | AB=A′B′,BC=B′C′,△ABC的周长等于△A′B′C′的周长 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com