
 如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )
如图,关于x的二次函数y=x2-x+m的图象交x轴的正半轴于A,B两点,交y轴的正半轴于C点,如果x=a时,y<0,那么关于x的一次函数y=(a-1)x+m的图象可能是( )| A. |  | B. | 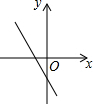 | C. |  | D. |  |
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{2}{9}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
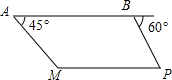 如图,我巡逻机在海岛M上空巡逻,距离海平面垂直高度为1000米,在A点测得正前方海岛M的俯角为45°,在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°,已知A,B,P,M在同一水平面上,求不明船只P与海岛M之间的距离(结果保留根号)
如图,我巡逻机在海岛M上空巡逻,距离海平面垂直高度为1000米,在A点测得正前方海岛M的俯角为45°,在沿海面水平方向飞行2000米到达B点时测得一不明船只P的俯角为60°,已知A,B,P,M在同一水平面上,求不明船只P与海岛M之间的距离(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
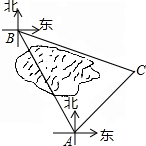 五一期间,小明同学到滨湖湿地公园参加校无线电测向科技社团组织的实践活动,目标点B在观测点A北偏西30°方向,距观测点A直线距离600米.由于观测点A和目标点B之间被一片湿地分隔,无法直接通行,小明根据地形决定从观测点A出发,沿东北方向走一段距离后,到达位于目标点B南偏东75°方向的C处,求小明还要走多远才能到达目标点B?(结果保留根号)
五一期间,小明同学到滨湖湿地公园参加校无线电测向科技社团组织的实践活动,目标点B在观测点A北偏西30°方向,距观测点A直线距离600米.由于观测点A和目标点B之间被一片湿地分隔,无法直接通行,小明根据地形决定从观测点A出发,沿东北方向走一段距离后,到达位于目标点B南偏东75°方向的C处,求小明还要走多远才能到达目标点B?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com