
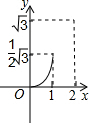
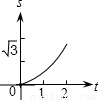
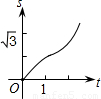
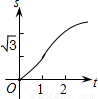
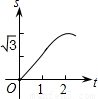
 如图,在直角坐标系的第一象限内,等边△ABO的边长为2,O为坐标原点,平行于y轴的动直线m沿OB方向平行移动,且与x轴相交于点D(x,0)(0≤x≤2),直线m截△ABO得直线m左侧的部分图形的面积y,那么y与x的函数关系图象大致是( )
如图,在直角坐标系的第一象限内,等边△ABO的边长为2,O为坐标原点,平行于y轴的动直线m沿OB方向平行移动,且与x轴相交于点D(x,0)(0≤x≤2),直线m截△ABO得直线m左侧的部分图形的面积y,那么y与x的函数关系图象大致是( )A、 | B、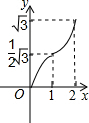 | C、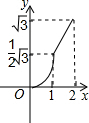 | D、 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| ||
| 2 |
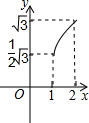


科目:初中数学 来源: 题型:
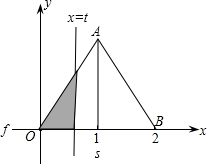 如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )
如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )A、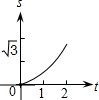 | B、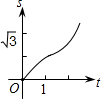 | C、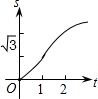 | D、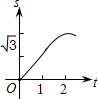 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系![]() 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,![]()
试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2010年高级中等学校招生全国统一考试数学卷(河北) 题型:解答题
如图,在直角坐标系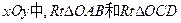 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
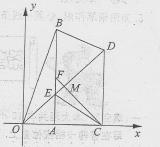
试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2008年江苏省淮安市淮阴中学高中招生考试数学试卷(解析版) 题型:选择题
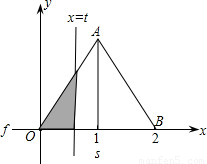
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com