
【题目】解方程:
(1)x2+x-3=0
(2)x2-6x=16
(3)2(x-3)=3x(x-3)
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)经过点(1,1)和(﹣1,0).下列结论:①a+c=1;②b2﹣4ac≥0;③当a<0时,抛物线与x轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为x=﹣![]() .其中结论正确的个数有( )
.其中结论正确的个数有( )
A.4 个B.3 个C.2 个D.1 个
查看答案和解析>>
科目:初中数学 来源: 题型:
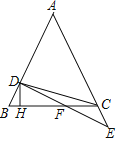
【题目】如图,在△ABC中,AB=AC,点D在AB上,点E在AC延长线上,且BD=CE,连接DE交BC于点F,作DH⊥BC于点H,连接CD.若tan∠DFH=![]() ,S△BCD=18,则DE的长为_____.
,S△BCD=18,则DE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
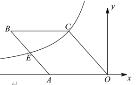
【题目】如图,在平面直角坐标系中,菱形 ABCO 的一边 OA 在 x 轴上,![]() ,反比例函数
,反比例函数![]() 过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
过菱形的顶点 C 和 AB 边上的中点E,则k的值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
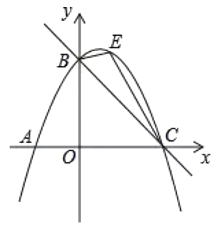
【题目】如图,直线![]() 与 x 轴交于点 C,与 y 轴交于点 B,抛物线
与 x 轴交于点 C,与 y 轴交于点 B,抛物线 ![]() 经过 B、C 两点.
经过 B、C 两点.
(1)求抛物线的解析式;
(2)如图,点 E 是抛物线上的一动点(不与 B,C 两点重合),△BEC 面积记为 S,当 S 取何值时,对应的点 E 有且只有三个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(x,|x﹣y|),则称点Q为点P的“关联点”.
(1)请直接写出点(2,2)的“关联点”的坐标;
(2)如果点P在函数y=x﹣1的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱![]() 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
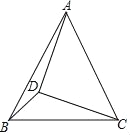
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com