【题目】如图，已知正比例函数y=3x的图象与反比例函数y=
的图象交于点A（1，m）和点B．
（1）求m的值和反比例函数的解析式．
（2）观察图象，直接写出使正比例函数的值大于反比例函数的值的自变量x的取值范围．
【答案】（1）m的值是3，反比例函数的解析式是y=
；（2）使正比例函数的值大于反比例函数的值的自变量x的取值范围是：﹣1＜x＜0或x＞1．
【解析】试题分析：（1）把A（1，m）代入y=3x求出m；把A的坐标代入y=
，即可求出反比例函数的解析式；
（2）根据图象和A、B的横坐标即可得出答案．
试题解析：（1）把A（1，m）代入y=3x得：m=3，
∴A（1，3），
把A的坐标代入y=
得：k=3，
则反比例函数的解析式是y=
．
答：m的值是3，反比例函数的解析式是y=
；
（2）解
得： 
， 
，
∴B（﹣1，﹣3），
∴使正比例函数的值大于反比例函数的值的自变量x的取值范围是：﹣1＜x＜0或x＞1．
科目：初中数学 来源： 题型：
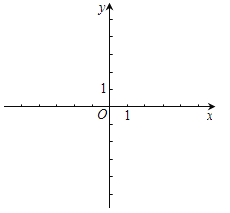
【题目】（（2016北京市）在平面直角坐标系xOy中，抛物线
（m＞0）与x轴的交点为A，B．
（1）求抛物线的顶点坐标；
（2）横、纵坐标都是整数的点叫做整点．
①当m＝1时，求线段AB上整点的个数；
②若抛物线在点A，B之间的部分与线段AB所围成的区域内（包括边界）恰有6个整点，结合函数的图象，求m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】九年级某班40位同学的年龄如下表所示：
年龄（岁） | 13 | 14 | 15 | 16 |
人数 | 3 | 16 | 19 | 2 |
则该班40名同学年龄的众数和中位数分别是（ ）
A.19，15
B.15，14.5
C.19，14.5
D.15，15
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数
（a＞0）图象的顶点为D，其图象与x轴的交点A、B的横坐标分别为﹣1和3，则下列结论正确的是（ ）
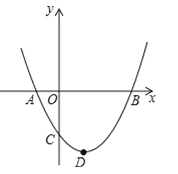
A．2a﹣b=0
B．a+b+c＞0
C．3a﹣c=0
D．当a=
时，△ABD是等腰直角三角形
查看答案和解析>>
科目：初中数学 来源： 题型：
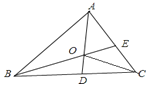
【题目】如图，AD和BE是△ABC的角平分线且交于点O，连接OC，现有以下论断： ①OD⊥BC；②∠AOC=90°+ 
∠ABC；③OA=OB=OC；④OC平分∠ACB；⑤∠AOE+∠DCO=90°其中正确的有____
查看答案和解析>>
科目：初中数学 来源： 题型：
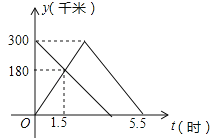
【题目】甲、乙两车分别从A、B两地同时出发，甲车匀速前往B地，到达B地立即以另一速度按原路匀速返回到A地；乙车匀速前往A地，设甲、乙两车距A地的路程为y（千米），甲车行驶的时间为x（时），y与x之间的函数图象如图所示
（1）求甲车从A地到达B地的行驶时间；
（2）求甲车返回时y与x之间的函数关系式，并写出自变量x的取值范围；
（3）求乙车到达A地时甲车距A地的路程．
查看答案和解析>>
科目：初中数学 来源： 题型：
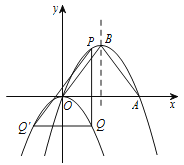
【题目】如图，在平面直角坐标系中．有抛物线
和
.抛物线
经过原点，与x轴正半轴交于点A，与其对称轴交于点B．P是抛物线上一点，且在x轴上方．过点P作x轴的垂线交抛物线
于点Q．过点Q作PQ的垂线交抛物线于点
（不与点Q重合），连结
.设点P的横坐标为m．
（1）求a的值；
（2）当抛物线经过原点时，设△
与△OAB重叠部分图形的周长为l．
①求
的值；
②求l与m之间的函数关系式；
（3）当h为何值时，存在点P，使以点O、A、Q、
为顶点的四边形是轴对称图形？直接写出h的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
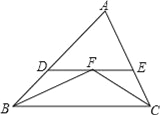
【题目】如图，△ABC中，∠ABC与∠ACB的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，那么下列结论：
①△BDF和△CEF都是等腰三角形；
②DE=BD+CE；
③△ADE的周长等于AB与AC的和；
④BF=CF．
其中正确的有（ ）
A. ①②③ B. ①②③④ C. ①② D. ①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com