
 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{6}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 连接BP.由正方形的对称性可知PD=PB,则PD+PE=PB+PE,依据两点之间线段最短可知当点B、P、E在一条直线上时,PD+PE有最小值,最小值=BE,然后依据正方形和等边三角形的性质求解即可
解答 解:连接BP.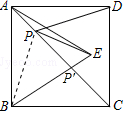
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE.
∴由两点之间线段最短可知当点P为点P′处时,PD+PE有最小值,最小值=BE.
∵正方形ABCD的面积为12,
∴AB=2$\sqrt{3}$.
又∵△ABE是等边三角形,
∴BE=AB=2$\sqrt{3}$.
∴PD+PE的最小值为2$\sqrt{3}$.
故选:D.
点评 本题主要考查的是正方形的性质、轴对称-最短路径问题,等边三角形的性质,等腰三角形的性质,明确当点P、E、B在一条直线上是,PE+PD有最小值是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,点C在线段AB上,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,点M、N分别是AC、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-3)2=9 | B. | (x-3)2=13 | C. | (x+3)2=5 | D. | (x-3)2=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1+x+x2=21 | B. | x2+2x=21 | C. | x(x-1)=21 | D. | $\frac{1}{2}$x(x-1)=21 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(-1,2),B(-3,4),C(-2,9).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个能储水30升的电热水器,安装有一个进水管和一个出水管,进出水管每单位时间内进出的水量各自是一个定值.设从某时刻开始的4分钟内只补充进水而不出水,在随后的8分钟内出水的同时补充进水,得到容器中剩余水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息回答下列问题:
一个能储水30升的电热水器,安装有一个进水管和一个出水管,进出水管每单位时间内进出的水量各自是一个定值.设从某时刻开始的4分钟内只补充进水而不出水,在随后的8分钟内出水的同时补充进水,得到容器中剩余水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com