练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB是半圆O的直径，C是半圆O上一点，弦AD平分∠BAC，交BC于点E，若AB=6，AD=5，则DE的长为 ．

    【答案】
    【解析】解：如图，连接BD，
    ∵AB为⊙O的直径，AB=6，AD=5，
    ∴∠ADB=90°，
    ∴BD= = ，
    ∵弦AD平分∠BAC，
    ∴ ，
    ∴∠DBE=∠DAB，
    在△ABD和△BED中，
    ，
    ∴△ABD∽△BED，
    ∴ ，即BD2=ED×AD，
    ∴（ ）2=ED×5，
    解得DE= ．
    所以答案是： ．

    【考点精析】通过灵活运用勾股定理的概念和圆周角定理，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半即可以解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

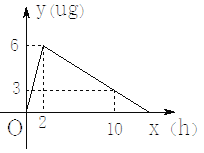
    【题目】某医药研究生开发了一种新药，在实验药效时发现，如果成人按规剂量服用，那么服用药后2h时血液中含药量最高，达每毫升6ug，接着逐步衰减，10h时血液中含药量每毫升3ug，每毫升血液中含药量y（ug）随时间x（h）的变化如图所示，当成人按规定剂量服药后.

    （1）分别求出x≤2和x>2时，y与x之间的函数关系式；

    （2）如果每毫升血液含药量为4ug或4ug以上时在治疗疾病时是有效的，那么这个有效时间是多长？每天至少吃几次药疗效最好？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四川雅安发生地震后，某校学生会向全校1900名学生发起了“心系雅安”捐款活动，为了解捐款情况，学生会随机调查了部分学生的捐款金额，并用得到的数据绘制了如下统计图①和图②，请根据相关信息，解答下列是问题：

    （1）本次接受随机抽样调查的学生人数为 ，图①中m的值是 ；

    （2）求本次调查获取的样本数据的平均数、众数和中位数；

    （3）根据样本数据，估计该校本次活动捐款金额为10元的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形 ABCD 中，点 G 是边 CD 上一点（不与端点 C，D 重合），以 CG为边在正方形 ABCD 外作正方形 CEFG，且 B、C、E 三点在同一直线上，设正方形 ABCD 和正方形 CEFG 的边长分别为 a 和 b．

    （1）分别用含 a，b 的代数式表示图 1 和图 2 中阴影部分的面积 S1、S2；

    （2）如果 a+b=5，ab=3，求 S1 的值；

    （3）当 S1＜S2 时，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算:

    (1) (－4x2y)·(－x2y2)·(y)3； (2) (－3ab)(2a2b＋ab－1) ；

    (3) (m－)(m＋)； （4） （-x-1）(-x+1) ； (5) ( - x - 5)2 ； （6） ；

    （7）先化简，再求值：（x+1）2﹣（x+2）（x﹣2），其中 ；

    (8)解方程组.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，锐角△ABC中，∠ACB=30°，AB=5，△ABC的面积为23．

    （1）若点P在AB边上且CP=，D，E分别为边AC，BC上的动点．求△PDE周长的最小值；

    （2）假设一只小羊在△ABC区域内，从路边AB某点出发跑到水沟边AC喝水，然后跑向路边BC吃草，再跑回出发点处休息，直接写出小羊所跑的最短路程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P是直线上一定点，点A是x轴上一动点不与原点重合，连接PA，过点P作，交y轴于点B，探究线段PA与PB的数量关系．

    1如图，当轴时，观察图形发现线段PA与PB的数量关系是______；

    2当PA与x轴不垂直时，在图中画出图形，线段PA与PB的数量关系是否与Ⅰ所得结果相同？写出你的猜想并加以证明；

    3 为何值时，线段？此时的度数是多少，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=a（x-2）2+c（a＞0），当自变量x分别取 、3、0时，对应的函数值分别：y1 ， y2 ， y3 ， 则y1 ， y2 ， y3的大小关系正确的是（　　）
    A.y3<y2<y1
    B.y1<y2<y3
    C.y2<y1<y3
    D.y3<y1<y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数y=（x-a）（x-b）（其中a＞b）的图象如下面图所示，则函数y=ax+b的图象可能正确的是（　　）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    同步练习册答案