
| 1 |
| 2 |
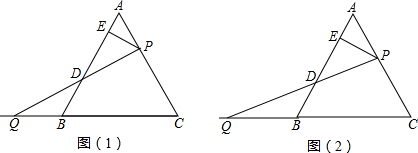
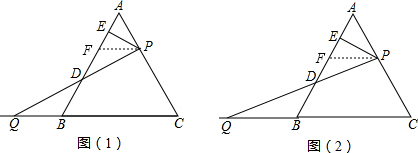 解:(1)如图(1),作PF∥BC交AB于点F,
解:(1)如图(1),作PF∥BC交AB于点F,
|
| 1 |
| 3 |
| 1 |
| 2 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
 某幼儿园为了增加幼儿的安全性,决定将园内滑梯的倾斜角由60°降为45°,原滑梯AB长为2米,考虑滑梯的正前面要留有空地保证安全性,滑梯的底部BC不动,只有将滑梯的高度降低,滑梯的高度应该降低多少米?(参考数据
某幼儿园为了增加幼儿的安全性,决定将园内滑梯的倾斜角由60°降为45°,原滑梯AB长为2米,考虑滑梯的正前面要留有空地保证安全性,滑梯的底部BC不动,只有将滑梯的高度降低,滑梯的高度应该降低多少米?(参考数据| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图,二次函数y=
已知:如图,二次函数y=| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 6 |
| 2 |
| 3 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米.小亮在胜利街的A处,测得此时AM为12米,求此时小亮距建筑物拐角D处有多远?
如图,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N,步行街宽MN为13.4米,建筑物宽DE为6米,光明巷宽EN为2.4米.小亮在胜利街的A处,测得此时AM为12米,求此时小亮距建筑物拐角D处有多远?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com