
 已知反比例函数y=$\frac{k}{x}$,经过点E(3,4),现请你在反比例函数y=$\frac{k}{x}$上找出一点P,使∠POE=45°,则此点P的坐标为(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$).
已知反比例函数y=$\frac{k}{x}$,经过点E(3,4),现请你在反比例函数y=$\frac{k}{x}$上找出一点P,使∠POE=45°,则此点P的坐标为(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$). 分析 过点E作EA⊥x轴于点A,过点P作PB⊥x轴于点B,由点E在反比例函数图象上得出k=12,设点P的坐标为(n,$\frac{12}{n}$),通过分割图形求出△OEP的面积,再根据面积公式表示出△OEP的面积,由此即可得出关于n的一元四次方程,结合函数图象解方程即可得出结论.
解答 解:方法一、过点E作EA⊥x轴于点A,过点P作PB⊥x轴于点B,如图所示.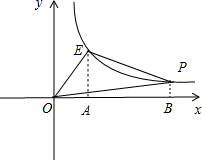
∵点E(3,4)在函数y=$\frac{k}{x}$的图象上,
∴k=3×4=12,
∴设点P的坐标为(n,$\frac{12}{n}$),则点A(3,0),点B(n,0),
S四边形OBPE=S△OAE+S梯形PBAE=$\frac{1}{2}$|k|+$\frac{1}{2}$(PB+EA)•AB=6+$\frac{1}{2}$($\frac{12}{n}$+4)(n-3)=2n-$\frac{18}{n}$+6.
S△OEP=S四边形OBPE-S△OBP=2n-$\frac{18}{n}$+6-$\frac{1}{2}$|k|=2n-$\frac{18}{n}$.
由两点间的距离公式可知:
OE=$\sqrt{{3}^{2}+{4}^{2}}$=5,OP=$\sqrt{{n}^{2}+(\frac{12}{n})^{2}}$,
S△OEP=$\frac{1}{2}$OE•OP•sin∠EOP=$\frac{5\sqrt{2}}{4}$$\sqrt{{n}^{2}+(\frac{12}{n})^{2}}$=2n-$\frac{18}{n}$,
即7n4-576n2-1008=0,
解得:n2=84或n2=-84(舍去),
∴n1=2$\sqrt{21}$,n2=-2$\sqrt{21}$(舍去).
∴点P的坐标为(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$);
方法二、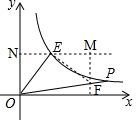
如图,过点E作EF⊥OE交OP于点F,过点E作EN⊥y轴,垂足为N,过点F作FM⊥NE于点M,
∴∠ONE=∠EMF=90°,
∴∠NOE+∠OEN=90°,
∵∠OEF=90°,
∴∠OEN+∠FEM=90°,
∴∠NOE=∠MEF,
若∠POE=45°,则OE=EF,
在△ONE和△MEF中,
∵$\left\{\begin{array}{l}{∠ONE=∠EMF=90°}\\{∠NOE=∠MEF}\\{OE=EF}\end{array}\right.$,
∴△ONE≌△MEF(AAS),
∴EM=ON=4、MF=NE=3,
则点F的坐标为(7,1),
∴直线OF的解析式为y=$\frac{1}{7}$x,
由$\left\{\begin{array}{l}{y=\frac{1}{7}x}\\{y=\frac{12}{x}}\end{array}\right.$,解得x=2$\sqrt{21}$或x=-2$\sqrt{21}$(舍),
当x=2$\sqrt{21}$时,y=$\frac{12}{x}$=$\frac{12}{2\sqrt{21}}$=$\frac{6\sqrt{21}}{21}$,
即点P(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$),
故答案为:(2$\sqrt{21}$,$\frac{6\sqrt{21}}{21}$).
点评 本题考查了反比例函数图象上点的坐标特征以及解一元高次方程,解题的关键是得出关于n的一元四次方程.本题属于中档题,难道不大,但较繁琐,解决该题型题目时,根据三角形面积的不同求法得出关于n的一元高次方程是关键.


科目:初中数学 来源: 题型:解答题
| 生产A种型号零件/件 | 生产B种型号零件/件 | 总时间/分 |
| 2 | 2 | 64 |
| 6 | 4 | 168 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,双曲线y=$\frac{k}{x}$的图象经过A(1,2)、B(2,b)两点.
已知:如图,双曲线y=$\frac{k}{x}$的图象经过A(1,2)、B(2,b)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com