
 如图1,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置上,∠EFB=67°,则∠AED′等于( )
如图1,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置上,∠EFB=67°,则∠AED′等于( )科目:初中数学 来源: 题型:
 如图1,把一个长为m、宽为n的长方形(m>n)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长(用含m,n的式子表示)为
如图1,把一个长为m、宽为n的长方形(m>n)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长(用含m,n的式子表示)为查看答案和解析>>
科目:初中数学 来源:学习周报 数学 人教课标七年级版 2009-2010学年 第19-26期 总第175-182期 人教课标版 题型:013
如图
1,把一个长为m、宽为n的长方形(m>n)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为
![]()
m-n
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
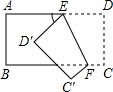 如图1,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置上,∠EFB=67°,则∠AED′等于
如图1,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置上,∠EFB=67°,则∠AED′等于查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图1,把一个长为m、宽为n的长方形(m>n)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长(用含m,n的式子表示)为________.
如图1,把一个长为m、宽为n的长方形(m>n)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长(用含m,n的式子表示)为________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com