练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图.AB是的直径，延长AB至P。使BP=OB. BD垂直于弦BC.垂足为点B.点D在PC上_设∠PCB=a.

    求证:



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图1，正六边形ABCDEF的边长为a，P是BC边上一动点，过P作PM∥AB交AF于M，作PN∥CD交DE于N，

    （1）∠MPN=       

    （2）求证：PM+PN=3a

    （2）如图2，点O是AD的中点，连接OM、ON。求证：OM=ON

     


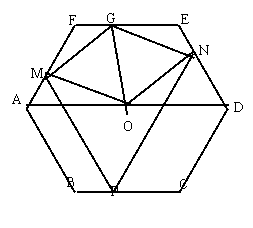    （3）如图3，点O是AD的中点，OG平分∠MON，判断四边形OMGN是否为特殊四边形，并说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：，其中．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


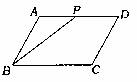
    如图，点P是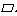ABCD边上一动点.沿A- D- C-B的路径移动，设P点经过的路径长为x,△BAP的面积是Y, 则下列能大致反映，y与x的函数关系的图象是

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    其中x为数据0,-1.-3,1.2的极差

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用矩形纸片折出直角的平分线，下列折法正确的是

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如果一个多面体的一个面是多边形，其余各面是有一个公共顶点的三角形，那么这个多面体叫做棱锥。如图是一个四棱柱和一个六棱锥，它们各有12条棱，下列棱柱中和九棱锥的棱数相等的是

    A. 五棱柱         B. 六棱柱         C. 七棱柱         D. 八棱柱

    查看答案和解析>>

    科目：初中数学 来源： 题型：


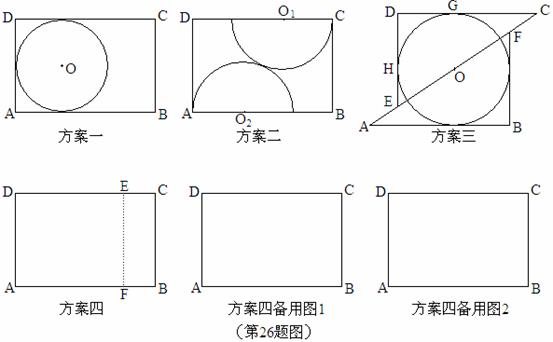
    木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：

    方案一：直接锯一个半径最大的圆；

    方案二：圆心O1，O2分别在CD，AB上，半径分别是O1C，O2A，锯两个外切的半圆拼成一个圆；

    方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；

    方案四：锯一块小矩形BCEF拼接到矩形AEFD下面，并利用拼成的木板锯一个尽可能大的圆。

    （1）写出方案一中的圆的半径；

    （2）通过计算说明方案二和方案三中，哪个圆的半径较大？

    （3）在方案四中，设CE=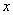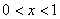（），圆的半径为，

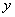    ①求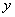关于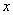的函数解析式；

    ②当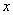取何值时圆的半径最大？最大半径是多少？并说明四种方案中，哪一个圆形桌面的半径最大？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


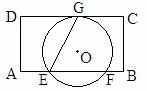
    如图，在矩形ABCD中，AD=8，E是边AB上一点，且AE=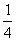AB，⊙O经过点E，与边CD所在直线相切于点G（∠GEB为锐角），与边AB所在直线相较于另一点F，且EG：EF=。当边AD或BC所在的直线与⊙O相切时，AB的长是     

    查看答案和解析>>

    同步练习册答案