
【题目】如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线y=x2+bx+c经过A、C两点.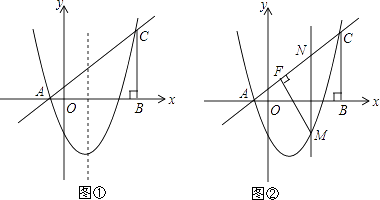
(1)求抛物线的解析式及其顶点坐标;
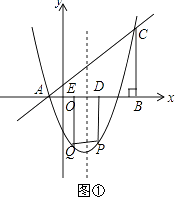
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P,Q分别向x轴作垂线,垂足为点D,E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
【答案】
(1)
解:由已知得:A(﹣1,0)、C(4,5),
∵二次函数y=x2+bx+c的图象经过点A(﹣1,0)C(4,5),
∴ ![]() ,
,
解得 ![]() .
.
∴抛物线解析式为y=x2﹣2x﹣3,
∵y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4)
(2)
解:由(1)知抛物线的对称轴为直线x=1,
设点P为(t,t2﹣2t﹣3),﹣1<t<3
∵P、Q为抛物线上的对称点,
∴PQ=2|t﹣1|,
当t>1时,d=2[2(t﹣1)+(﹣t2+2t+3)]=﹣2t2+8t+2=﹣2(t﹣2)2+10,
∵﹣2<0,
∴当t=2时,d有最大值为10,即P(2,﹣3);
当t<1时,由抛物线的对称性得,点P为(0,﹣3)时,d有最大值10,;
综上,当P为(0,﹣3)或(2,﹣3)时,d有最大值10
(3)
解:过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°,
∵MF⊥AC,
∴FH= ![]() MN,
MN,
∴ ![]() =
= ![]() =
= ![]() ,
,
∵A(﹣1,0,C(4,5),
∴直线AC的解析式为y=x+1,
设M(m,m2﹣2m﹣3),其中﹣1<m<4,则CG=4﹣m,
由MN∥BC得,N(m,m+1),
∴MN的长为:(m+1)﹣(m2﹣2m﹣3)=﹣m2+3m+4,
当 ![]() =
= ![]() 时,则3MN=4CG,即3(﹣m2+3m+4)=4(4﹣m),
时,则3MN=4CG,即3(﹣m2+3m+4)=4(4﹣m),
解得m1= ![]() ,m2=4(舍去),
,m2=4(舍去),
∴M( ![]() ,﹣
,﹣ ![]() ),
),
当 ![]() =
= ![]() 时,则2MN=6CG,即2(﹣m2+3m+4)=6(4﹣m),
时,则2MN=6CG,即2(﹣m2+3m+4)=6(4﹣m),
解得m3=2,m4=4(舍去),
∴M(2,﹣3).
综上,当M的坐标为( ![]() ,﹣
,﹣ ![]() )或(2,﹣3)时,MN将△MFC的面积分成2:3两部分.
)或(2,﹣3)时,MN将△MFC的面积分成2:3两部分.
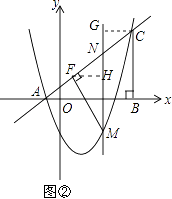
【解析】(1)利用待定系数法即可求得抛物线的解析式,进而转化成顶点式,求得顶点坐标即可;(2)设点P为(t,t2﹣2t﹣3),﹣1<t<3,因为对称轴x=1,所以PQ=2|t﹣1|,然后分三种情况讨论即可求得;(3)过点F作FH⊥MN于H,过C作CG⊥MN于G,则∠ANM=∠ACB=45°,进而求得FH= ![]() MN,从而得出
MN,从而得出 ![]() =
= ![]() =
= ![]() ,根据A、C的坐标求得直线AC的解析式为y=x+1,设M(m,m2﹣2m﹣3),其中﹣1<m<4,则CG=4﹣m,由MN∥BC得N(m,m+1),求得MN的长为:(m+1)﹣(m2﹣2m﹣3)=﹣m2+3m+4,然后分两种情况:当
,根据A、C的坐标求得直线AC的解析式为y=x+1,设M(m,m2﹣2m﹣3),其中﹣1<m<4,则CG=4﹣m,由MN∥BC得N(m,m+1),求得MN的长为:(m+1)﹣(m2﹣2m﹣3)=﹣m2+3m+4,然后分两种情况:当 ![]() =
= ![]() 时,则3MN=4CG;当
时,则3MN=4CG;当 ![]() =
= ![]() 时,则2MN=6CG;列出关于m的方程,解方程即可求得M的坐标.
时,则2MN=6CG;列出关于m的方程,解方程即可求得M的坐标.
【考点精析】解答此题的关键在于理解二次函数的概念的相关知识,掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数,以及对二次函数的图象的理解,了解二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】利用直尺和圆规作一个角等于已知角的作法如下:
①以点O为圆心,以任意长为半径画弧,分别交OA、OB于点D、C;
②作射线O′B′,以点O′为圆心,以 长为半径画弧,交O′B′于点C′;
③以点C′为圆心,以 长为半径画弧,两弧交于点D′;
④过点D′作射线O′A′,∴∠A′O′B′为所求.
(1)请将上面的作法补充完整;
(2)△OCD≌△O′C′D′的依据是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
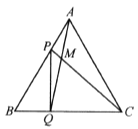
【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第![]() s或
s或![]() s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有分别标有数字1,2,3,4四个小球,除数字不同外,小球没有任何区别,每次实验先搅拌均匀.
(1)若从中任取一球,球上的数字为偶数的概率为多少?
(2)若从中任取一球(不放回),再从中任取一球,请用画树状图或列表格的方法求出两个球上的数字之和为偶数的概率.
(3)若设计一种游戏方案:从中任取两球,两个球上的数字之差的绝对值为1为甲胜,否则为乙胜,请问这种游戏方案设计对甲、乙双方公平吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,AD⊥BC于D,且AD=BC=4,若将三角形沿AD剪开成为两个三角形,在平面上把这两个三角形拼成一个四边形,你能拼出所有的不同形状的四边形吗?画出所拼四边形的示意图(标出图中的直角),并分别写出所拼四边形的对角线的长.(只需写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BDE中,∠BDE=90°,BD=6 ![]() ,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 .
,点D的坐标是(7,0),∠BDO=15°,将△BDE旋转到△ABC的位置,点C在BD上,则旋转中心的坐标为 . 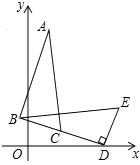
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形. 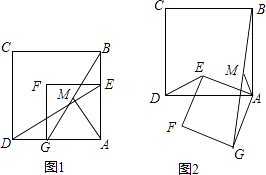
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店老板去批发市场购买某种图书.第一次用1200元购书若干本,并按该书定价20元出售,很快售完.由于该书畅销,第二次购书时,每本书批发价比第一次提高了25%,他用1800元所购该书数量比第一次多20本,又按定价售出全部图书.
(1)求该书原来每本的批发价;
(2)该老板这两次售书一共赚了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com