
 (1)抛物线的顶点在原点,且经过点(-2,8),求该抛物线的解析式.
(1)抛物线的顶点在原点,且经过点(-2,8),求该抛物线的解析式.分析 (1)设二次函数的解析式为y=ax2(a≠0),再把点(-2,8)代入求出a的值即可;
(2)根据函数图象的顶点坐标可得出其最小值,再由函数图象经过原点,对称轴为直线x=-3可得出P点坐标,由函数图形可得出x>-3时函数的增减性.
解答 解:(1)设二次函数的解析式为y=ax2(a≠0),
∵点(-2,8)在此函数的图象上,
∴4a=8,解得a=2,
∴抛物线的解析式为:为y=2x2;
(2)∵抛物线y=ax2+bx的顶点为A(-3,-3),
∴y的最小值=-3;
∵抛物线经过原点,对称轴为x=-3,
∴t=-6,
∴P(-6,0).
由函数图象可知,当x>-3时,y随x的增大而增大.
故答案为:-3,(-6,0),增大.
点评 本题考查的是用待定系数法求二次函数的解析式,能利用函数图象得出其顶点坐标、对称轴方程及增减性是解答此题的关键.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
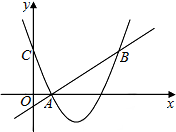 如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该函数图象对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
如图,二次函数y=(x-2)2+m的图象与y轴交于点C,点B是点C关于该函数图象对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,篮球运动员小明站在距端线4米的O处长传球,球从离地面1米的A处扔出,划出一条漂亮的抛物线,篮球在距O点6米的B处达到最高点,最高点C距地面4米,篮球在D处落地后,又一次弹起,据试验,篮球在场地上第二次弹起后划出的抛物线与第一次划出的抛物线形状相同,但最大高度减少到原来最大高度的一半,以小明站立处O为坐标原点,建立平面直角坐标系如图所示.
如图,篮球运动员小明站在距端线4米的O处长传球,球从离地面1米的A处扔出,划出一条漂亮的抛物线,篮球在距O点6米的B处达到最高点,最高点C距地面4米,篮球在D处落地后,又一次弹起,据试验,篮球在场地上第二次弹起后划出的抛物线与第一次划出的抛物线形状相同,但最大高度减少到原来最大高度的一半,以小明站立处O为坐标原点,建立平面直角坐标系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com