
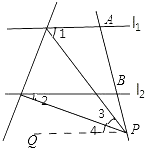
【题目】如图,已知直线l1∥l2 , 且l3和l1、l2分别交于A,B两点,点P在AB上. 
(1)试找出∠1、∠2、∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动时,问∠1、∠2、∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动时,试探究∠1、∠2、∠3之间的关系(点P和A,B不重合)
【答案】
(1)解:∠1+∠2=∠3;
理由:过点P作l1的平行线,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)
∵∠4+∠5=∠3,
∴∠1+∠2=∠3
(2)解:同(1)可证:∠1+∠2=∠3
(3)解:∠1﹣∠2=∠3或∠2﹣∠1=∠3
理由:当点P在下侧时,过点P作l1的平行线PQ,
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)
∴∠1﹣∠2=∠3;
当点P在上侧时,同理可得:∠2﹣∠1=∠3.
【解析】(1)过点P作l1的平行线,根据平行线的性质进行解题.(2)(3)都是同样的道理. 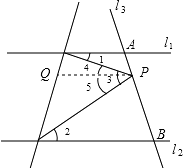
【考点精析】认真审题,首先需要了解平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补).


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】小明在计算A-2(ab+2bc-4ac)时,由于马虎,将“A-”写成了“A+”,得到的结果是3ab-2ac+5bc。试问:假如小明没抄错时正确的结果是多少。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC经过平移得到的△A′B′C′,△ABC中任意一点P(x1 , y1)平移后的对应点为P′(x1+6,y1+4). 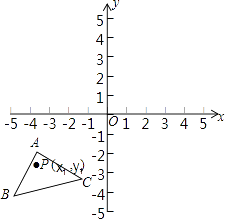
(1)请在图中作出△A′B′C′;
(2)写出点A′、B′、C′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 有一个外角是120°的等腰三角形是等边三角形
B. 等边三角形有3条对称轴
C. 有两边和一角对应相等的两个三角形全等
D. 有一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长方形的一边长等于3m+2n,其邻边长比它长m-n,则这个长方形的周长是( )
A. 14m+6n B. 7m+3n
C. 4m+n D. 8m+2n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个直角∠AOB,∠COD有相同的顶点O,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的个数有( ) 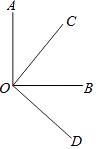
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=![]() .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④0<CE≤6.4.其中正确的结论是______________.(填序号)
;④0<CE≤6.4.其中正确的结论是______________.(填序号) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com