
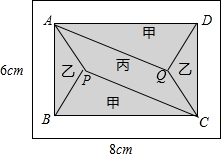
 小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.
小黄准备给长8m,宽6m的长方形客厅铺设瓷砖,现将其划分成一个长方形ABCD区域Ⅰ(阴影部分)和一个环形区域Ⅱ(空白部分),其中区域Ⅰ用甲、乙、丙三种瓷砖铺设,且满足PQ∥AD,如图所示.分析 (1)根据题意可得300S+(48-S)200≤12000,解不等式即可;
(2)①设区域Ⅱ四周宽度为a,则由题意(6-2a):(8-2a)=2:3,解得a=1,由此即可解决问题;
②设乙、丙瓷砖单价分别为5x元/m2和3x元/m2,则甲的单价为(300-3x)元/m2,由PQ∥AD,可得甲的面积=矩形ABCD的面积的一半=12,设乙的面积为s,则丙的面积为(12-s),由题意12(300-3x)+5x•s+3x•(12-s)=4800,解得s=$\frac{600}{x}$,由0<s<12,可得0<$\frac{600}{x}$<12,解不等式即可;
解答 解:(1)由题意300S+(48-S)200≤12000,
解得S≤24.
∴S的最大值为24.
(2)①设区域Ⅱ四周宽度为a,则由题意(6-2a):(8-2a)=2:3,解得a=1,
∴AB=6-2a=4,CB=8-2a=6.
②设乙、丙瓷砖单价分别为5x元/m2和3x元/m2,则甲的单价为(300-3x)元/m2,
∵PQ∥AD,
∴甲的面积=矩形ABCD的面积的一半=12,设乙的面积为s,则丙的面积为(12-s),
由题意12(300-3x)+5x•s+3x•(12-s)=4800,
解得s=$\frac{600}{x}$,
∵0<s<12,
∴0<$\frac{600}{x}$<12,又∵300-3x>0,
综上所述,50<x<100,150<3x<300,
∴丙瓷砖单价3x的范围为150<3x<300元/m2.
点评 本题考查不等式的应用、矩形的性质等知识,解题的关键是理解题意,学会构建方程或不等式解决实际问题,属于中考常考题型.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
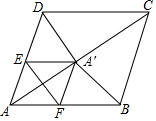 在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.
在菱形ABCD中,AB=5,AC=8,点P是对角线AC上的一个动点,过点P作EF垂直于AC交AD于点E,交AB于点F,将△AEF折叠,使点A落在点A′处,当△A′CD时等腰三角形时,AP的长为$\frac{3}{2}$或$\frac{39}{16}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4π | B. | 3π | C. | 2π | D. | π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线C1:y=ax2-4ax-5(a>0).
已知抛物线C1:y=ax2-4ax-5(a>0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
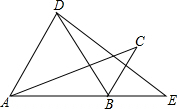 如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )
如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB延长线上,连接AD.下列结论一定正确的是( )| A. | ∠ABD=∠E | B. | ∠CBE=∠C | C. | AD∥BC | D. | AD=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江苏省启东市九年级寒假作业测试(开学考试)数学试卷(解析版) 题型:填空题
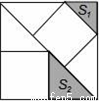
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com