
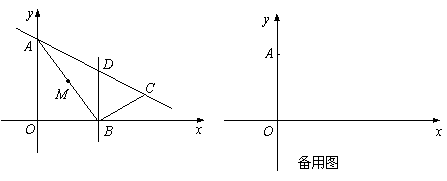
��ͼ����ƽ��ֱ������ϵ�У���A��0��6������B��x���ϵ�һ�����㣬����AB��ȡAB���е�M�����߶�MB���ŵ�B��˳ʱ�뷽����ת90o���õ��߶�BC.����B��x��Ĵ��߽�ֱ��AC�ڵ�D.���B�����ǣ�t��0��.
��1����t=4ʱ����ֱ��AB�Ľ���ʽ��
��2����t>0ʱ���ú�t�Ĵ���ʽ��ʾ��C�����꼰��ABC�������
��3���Ƿ���ڵ�B,ʹ��ABDΪ����������?�����ڣ���������з��������ĵ�B�����ꣻ�������ڣ���˵������.
 |
�⣺��1����t=4ʱ��B(4,0)
��ֱ��AB�Ľ���ʽΪy= kx+b .
�� A(0,6)��B(4,0) ����ã�
![]() , ��ã�
, ��ã�![]() ,
,
��ֱ��AB�Ľ���ʽΪ��y=��![]() x+6.
x+6.
(2) ����C��CE��x���ڵ�E
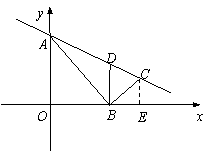 |
�ɡ�AOB=��CEB=90�㣬��ABO=��BCE���á�AOB�ס�BEC.
��![]() ��
��
��BE= ![]() AO=3��CE=
AO=3��CE= ![]() OB=
OB= ![]() ��
��
���C������Ϊ(t+3��![]() ).
).
����һ��
S����AOEC= ![]() OE?(AO+EC)=
OE?(AO+EC)= ![]() (t+3)(6+
(t+3)(6+![]() )=
)=![]() t2+
t2+![]() t+9��
t+9��
S�� AOB= ![]() AO?OB=
AO?OB= ![]() ��6?t=3t��
��6?t=3t��
S�� BEC= ![]() BE?CE=
BE?CE= ![]() ��3��
��3��![]() =
= ![]() t��
t��
��S�� ABC= S����AOEC�� S�� AOB��S�� BEC
= ![]() t2+
t2+![]() t+9��3t��
t+9��3t��![]() t
t ![]() =
= ![]() t2+9.
t2+9.
��������
��AB��BC��AB=2BC����S�� ABC= ![]() AB?BC= BC2.
AB?BC= BC2.
��Rt��ABC��BC2= CE2+ BE2 = ![]() t2+9��
t2+9��
��S�� ABC= ![]() t2+9.
t2+9.
(3)���ڣ��������£�
�ٵ�t��0ʱ.
��.��AD��BD.
�֡�BD��y��
���OAB=��ABD����BAD=��ABD��
���OAB=��BAD.
�֡ߡ�AOB=��ABC��
���ABO�ס�ACB��
��![]() ��
��
��![]() =
= ![]() ��
��
��t=3����B(3��0).
��.��AB��AD.
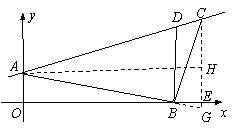
�ӳ�AB��CE���ڵ�G��
�֡�BD��CG
��AG��AC
����A��AH��CG��H��
 |
��CH��HG��![]() CG
CG
�ɡ�AOB�ס�GEB��
��![]() ��
��![]() ��
��
��GE= ![]() .
.
�֡�HE��AO������CE��![]()
��![]() ������
������![]() ����
����![]() ��
��![]() ��
��
��t2-24t-36=0
��ã�t=12��6![]() . ��Ϊ t��0��
. ��Ϊ t��0��
����t=12��6![]() ����B(12��6
����B(12��6![]() ��0).
��0).
��.����֪������֪����0��t<12ʱ����ADBΪ�۽ǣ���BD �� AB.
��t��12ʱ��BD��CE<BC<AB.
�൱t��0ʱ��������BD��AB�����.
�ڵ���3��t<0ʱ����ͼ����DAB�Ƕ۽�.
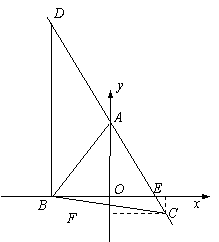 |
��AD=AB��
����C�ֱ���CE��x�ᣬCF��y���ڵ�E����F.
����õ�C������Ϊ(t+3��![]() )��
)��
��CF=OE=t+3��AF=6��![]() ��
��
��BD��y�ᣬAB=AD�ã�
��BAO=��ABD����FAC=��BDA����ABD=��ADB
���BAO=��FAC��
�֡ߡ�AOB=��AFC=90�㣬
���AOB�ס�AFC��
��![]() ��
��
�� �� ��t2-24t-36=0
�� ��t2-24t-36=0
��ã�t=12��6![]() .��Ϊ��3��t<0��
.����3��t<0��
����t=12��6![]() ����B (12��6
����B (12��6![]() ��0).
��0).
�۵�t<��3ʱ����ͼ��
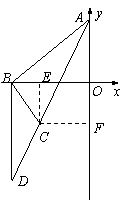 |
��ABD�Ƕ۽�.��AB=BD��
����C�ֱ���CE��x�ᣬCF��y���ڵ�E����F��
����õ�C������Ϊ(t+3��![]() )��
)��
��CF= ��(t+3)��AF=6��![]() ��
��
��AB=BD��
���D=��BAD.
�֡�BD��y�ᣬ
���D=��CAF��
���BAC=��CAF.
�֡ߡ�ABC=��AFC=90�㣬AC=AC��
���ABC�ա�AFC��
��AF��AB��CF=BC��
��AF=2CF����6��![]() =��2(t+3)��
=��2(t+3)��
��ã�t=��8����B(��8��0).
�������������ڵ�Bʹ��ABDΪ���������Σ���ʱ��B����Ϊ��
B1 (3��0)��B2 (12��6![]() ��0)��B3 (12��6
��0)��B3 (12��6![]() ��0)��B4(��8��0).
��0)��B4(��8��0).


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��| BD |
| AB |
| 5 |
| 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����| 5 |
| 29 |
| 5 |
| 29 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=| k |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com