
【题目】根据题意, 补全解题过程:
如图,∠AOB=90°,OE平分∠AOC,OF平分∠BOC. 求∠EOF的度数.
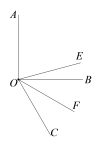
解:因为OE平分∠AOC,OF平分∠BOC
所以∠EOC =![]() ∠AOC,∠FOC =
∠AOC,∠FOC =![]() ________.
________.
所以∠EOF =∠EOC-________
=![]() (∠AOC-_______)
(∠AOC-_______)
=![]() ________
________
=_________°.
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
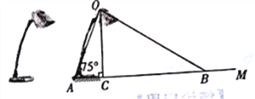
【题目】图为放置在水平桌面上的台灯的平面示意图,可伸缩式灯臂AO长为40 cm,与水平面所形成的夹角∠OAM恒为75°(不受灯臂伸缩的影响).由光源0射出的光线沿灯罩形成光线OC,OB,与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°.
(1)求该台灯照亮桌面的宽度BC.(不考虑其他因素,结果精确到1 cm,参考数据:sin75°≈0.97,cos75°≈0.26, ![]() ≈1.73)
≈1.73)
(2)若灯臂最多可伸长至60 cm,不调整灯罩的角度,能否让台灯照亮桌面85 cm的宽度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法:把两个全等的直角三角形如图1放置,其三边长分别为a、b、c,显然∠DAB=∠B=90°,AC⊥DE.
(1)请用a、b、c分别表示出梯形ABCD、四边形AECD、△EBC的面积,再通过探究这三个图形面积之间的关系,证明:勾股定理a2+b2=c2;
(2)如图2,铁路上A、B两点(看作直线上的两点)相距40千米,C、D为两个村庄(看作两个点),AD⊥AB,BC⊥AB,垂足分别为A、B,AD=24千米,BC=16千米,在AB上有一个供应站P,且PC=PD,求出AP的距离;
(3)借助(2)的思考过程与几何模型,直接写出代数式![]() 的最小值为 .
的最小值为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )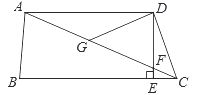
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠CAB=30°,BC=2,O、H分别为边AB、AC的中点,将△ABC绕点B顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过部分的面积(即阴影部分面积)为_____.
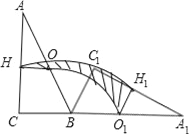
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小张某天下午的运营是在一条东西走向的大道上。如果规定向东为正,他这天下午的行程记录如下:(单位:千米)
+15,-3,+14,-11,+10,-18,+14
(1)将最后一名乘客送到目的地时,小张离下午出车点的距离是多少?
(2)离开下午出发点最远时是多少千米?
(3)若汽车的耗油量为0.06升/千米,油价为4.5元/升,这天下午共需支付多少油钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
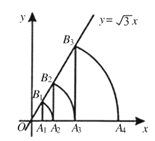
【题目】如图,已知直线y=![]() x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点A6的坐标为____________.
x,点A1的坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1的长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2的长为半径画弧交x轴于点A3,…,按此做法进行下去,则点A6的坐标为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com