
【题目】如图,点D在△ABC的边AC上,要判定△ADB与△ABC相似,需添加一个条件,则以下所添加的条件不正确的是( )

A.∠ABD=∠CB.∠ADB=∠ABCC.![]() =
=![]() D.
D.![]() =
=![]()
科目:初中数学 来源: 题型:
【题目】小丽和哥哥小明分别从家和图书馆同时出发,沿同一条路相向而行,小丽开始跑步,遇到哥哥后改为步行,到达图书馆恰好用35分钟,小明匀速骑自行车直接回家,骑行10分钟后遇到了妹妺,再继续骑行5分钟,到家两人距离家的路程y(m)与各自离开出发的时间x(min)之间的函数图象如图所示:
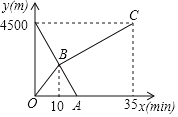
(1)求两人相遇时小明离家的距离;
(2)求小丽离距离图书馆500m时所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点M在BA的延长线上,MD切⊙O于点D,过点B作BN⊥MD于点C,连接AD并延长,交BN于点N.

(1)求证:AB=BN;
(2)若MD=4,CD=2.4,求![]() 。
。
(3)若AM=2,CN=1.2,求⊙O的半径长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与坐标轴交于A(﹣4,0)、B(2,0)、C(0,4),连接BC,AC.
(1)求抛物线的解析式;
(2)若点E是抛物线在第二象限上的一点,过点E作DE⊥AC于点D,求DE的最大值.
(3)若点E是抛物线上第二象限上的一动点,过点E作DE⊥AC于点D,连接CE,若△CDE与△COB相似,直接写出点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组的同学们,想利用自己所学的数学知识测量学校旗杆的高度:下午活动时间,兴趣小组的同学们来到操场,发现旗杆的影子有一部分落在了墙上(如图所示).同学们按照以下步骤进行测量:测得小明的身高1.65米,此时其影长为2.5米;在同一时刻测量旗杆影子落在地面上的影长BC为9米,留在墙上的影高CD为2米,请你帮助兴趣小组的同学们计算旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司在甲乙两地同时销售某种品牌的汽车,已知在甲地的总销售利润y(单位:万元)与销售量x(单位:辆)之间满足y=﹣![]() x2+10x,在乙地每销售一辆汽车可获得2万元的销售利润,若该公司在甲乙两地共销售30辆该品牌的汽车,甲乙两地总的销售利润为W万元,其中在甲地销售x辆.
x2+10x,在乙地每销售一辆汽车可获得2万元的销售利润,若该公司在甲乙两地共销售30辆该品牌的汽车,甲乙两地总的销售利润为W万元,其中在甲地销售x辆.
(1)求W与x的函数关系式;
(2)甲乙两地各销售多少辆车时W最大?W的最大值是多少?
(3)为了开拓甲地市场,公司规定甲地平均每辆汽车的销售利润不高于2万元,那么公司销售这30辆汽车可获得的最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )
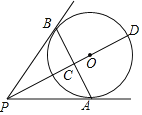
A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
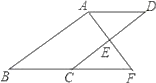
【题目】如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com