
【题目】如图,在△ABC中,AB=AC=4,AF⊥BC于点F,BH⊥AC于点H.交AF于点G,点D在直线AF上运动,BD=DE,∠BDE=135°,∠ABH=45°,当AE取最小值时,BE的长为_____.
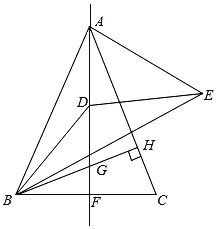
【答案】2![]() .
.
【解析】
如图,连接CG,CE.证明△DBG∽△EBC,推出∠BGD=∠BCE=112.5°,推出∠ACE=45°,推出点E的运动轨迹是直线EC,推出当AE⊥EC时,AE的值最小,再利用勾股定理求出BE即可.
如图,连接CG,CE.
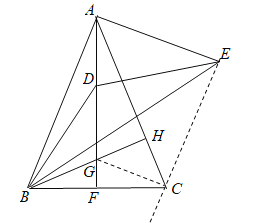
∵BH⊥AC,
∴∠BHA=90°,
∵∠ABH=45°,
∴∠BAC=45°,
∵AB=AC,AF⊥BC,
∴∠BAF=∠CAF=22.5°,BF=CF,
∴GB=GC,
∴∠BGF=∠CGF=67.5°,
∴∠GBF=∠GCF=22.5°,
∵DB=DE,∠BDE=135°,
∴∠DBE=∠DEB=22.5°,
∴∠DBE=∠GBC=∠DEB=∠GCF,
∴△DBE∽△GBC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵∠DBG=∠EBC,
∴△DBG∽△EBC,
∴∠BGD=∠BCE=112.5°,
∵∠ACB=67.5°,
∴∠ACE=45°,
∴点E的运动轨迹是直线EC,
∴当AE⊥EC时,AE的值最小,最小值=![]() AC=2
AC=2![]() ,
,
此时∠BAE=90°,BE=![]() =
=![]() =2
=2![]() ,
,
故答案为2![]() .
.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:初中数学 来源: 题型:
【题目】已知等腰△ABC的顶角∠A=36°(如图).
(1)请用尺规作图法作底角∠ABC的平分线BD,交AC于点D(保留作图痕迹,不要求写作法);
(2)证明:△ABC∽△BDC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,在平面直角坐标系xOy中,点A、B、C分别为坐标轴上上的三个点,且OA=1,OB=3,OC=4,
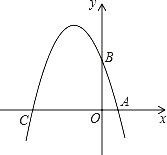
(1)求经过A、B、C三点的抛物线的解析式;
(2)在平面直角坐标系xOy中是否存在一点P,使得以以点A、B、C、P为顶点的四边形为菱形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点M为该抛物线上一动点,在(2)的条件下,请求出当|PM﹣AM|的最大值时点M的坐标,并直接写出|PM﹣AM|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() (其中
(其中![]() )的图像与
)的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
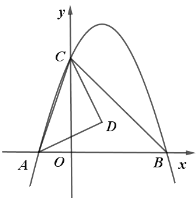
(1)点![]() 的坐标为 ,
的坐标为 ,![]()
![]() ;
;
(2)若![]() 为
为![]() 的外心,且
的外心,且![]() 与
与![]() 的面积之比为
的面积之比为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,试探究抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
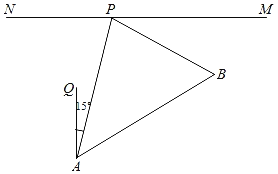
【题目】如图,在一条东西走向的公路MN的同侧有A,B两个村庄,村庄B位于村庄A的北偏东60°的方向上(∠QAB=60°),公路旁的货站P位于村庄A的北偏东15°的方向上,已知PA平分∠BPN,AP=2km,求村庄A,B之间的距离.(计算结果精确到0.01km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,PA是过正方形顶点A的直线,作DE⊥PA于E,将射线DE绕点D逆时针旋转45°与直线PA交于点F.
(1)如图1,当∠PAD=45°时,点F恰好与点A重合,则![]() 的值为 ;
的值为 ;
(2)如图2,若45°<∠PAD<90°,连接BF、BD,试求![]() 的值,并说明理由.
的值,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,
中,![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 轴的负半轴上,
轴的负半轴上,![]() ,
,![]() 在反比例函数
在反比例函数![]() (
(![]() )的图象上,
)的图象上,![]() 与
与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,若
,若![]() 的面积是3,则
的面积是3,则![]() 的值是_________.
的值是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com