
【题目】我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
(1)求W关于x的函数关系式,并写出自变量x的取值范围;
(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;
(3)“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.
【答案】
(1)解:∵甲团队人数为x人,乙团队人数不超过50人,
∴120﹣x≤50,
∴x≥70,
①当70≤x≤100时,W=70x+80(120﹣x)=﹣10x+9600,
②当100<x<120时,W=60x+80(120﹣x)=﹣20x+9600,
综上所述,W= ![]()
(2)解:∵甲团队人数不超过100人,
∴x≤100,
∴W=﹣10x+9600,
∵70≤x≤100,
∴x=70时,W最大=8900(元),
两团联合购票需120×60=7200(元),
∴最多可节约8900﹣7200=1700(元)
(3)解:∵x≤100,
∴W=(70﹣a)x+80(120﹣x)=﹣(a+10)x+9600,
∴x=70时,W最大=﹣70a+8900(元),
两团联合购票需120(60﹣2a)=7200﹣240a(元),
∵﹣70a+8900﹣(7200﹣240a)=3400,
解得:a=10
【解析】(1)根据题意可得到甲团队人数大于等于70,然后再分为70≤x≤100和100<x<120两种情况求解即可;
(2)由题意可知x≤100,则W=-10x+9600(70≤x≤100)然后再利用一次函数的图象和性质求得W的最大值即可;
(3)由每张门票降价a元,可得到W=(70-a)x+80(120-x)=-(a+10)x+9600,由一次函数的增减性可知:x=70时,W最大=-70a+8900(元),接下来,再求得两队团联合购票所需的费用,最后,依据甲乙两团队联合购票比分别购票最多节约3400元列方程求解即可.


科目:初中数学 来源: 题型:
【题目】中考体育测试前,某区教育局为了了解选报引体向上的初三男生的成绩情况,随机抽测了本区部分选报引体向上项目的初三男生的成绩,并将测试得到的成绩绘成了下面两幅不完整的统计图:
请你根据图中的信息,解答下列问题:
(![]() )写出扇形图中
)写出扇形图中![]() __________
__________![]() ,并补全条形图.
,并补全条形图.
(![]() )在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
)在这次抽测中,测试成绩的众数和中位数分别是__________个、__________个.
(![]() )该区体育中考选报引体向上的男生共有
)该区体育中考选报引体向上的男生共有![]() 人,如果体育中考引体向上达
人,如果体育中考引体向上达![]() 个以上(含
个以上(含![]() 个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?
个)得满分,请你估计该区体育中考中选报引体向上的男生能获得满分的有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)请在图①的正方形ABCD的对角线BD上作一点P,使PA+PC最小;
(2)如图②,点P为矩形ABCD的对角线BD上一动点,AB=2,BC=2 ![]() ,点E为BC边的中点,求作一点P,使PE+PC最小,并求这个最小值.
,点E为BC边的中点,求作一点P,使PE+PC最小,并求这个最小值.
(3)如图③,李师傅有一块边长为1000米的菱形ABCD采摘园,AC=1200米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出的点P位置,并求出这个最短距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,BC=5,点E,F分别在AB,CD上,将矩形ABCD沿EF折叠,使点A,D分别落在矩形ABCD外部的点A1,D1处,求阴影部分图形的周长.
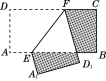
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在弹性限度内,弹簧挂上物体后会伸长,测得弹簧的长度 y(cm)与所挂物体的质量 x(kg)之间有如下表关系:

下列说法不正确的是( )
A.y 随 x 的增大而增大B.所挂物体质量每增加 1kg弹簧长度增加 0.5cm
C.所挂物体为 7kg时,弹簧长度为 13.5cmD.不挂重物时弹簧的长度为 0cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位自然数是![]() ,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数
,将它任意两个数位的数字对调后得到一个首位不为0的新三位自然数![]() (
(![]() 可以与
可以与![]() 相同),设
相同),设![]() ,在
,在![]() 所有的可能情况中,当
所有的可能情况中,当![]() 最大时,我们称此时的
最大时,我们称此时的![]() 是
是![]() 的“梦想数”,并规定
的“梦想数”,并规定![]() .例如127按上述方法可得到新数有:217、172、721,因为
.例如127按上述方法可得到新数有:217、172、721,因为![]() 所以172是172的“梦想数”,此时,
所以172是172的“梦想数”,此时,![]() .
.
(1)求512的“梦想数”及![]() 的值;
的值;
(2)设三位自然数![]() 交换其个位与十位上的数字得到新数
交换其个位与十位上的数字得到新数![]() ,若
,若![]() ,且
,且![]() 能被7整除,求
能被7整除,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= ![]() 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.
相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.
(1)求双曲线和抛物线的解析式;
(2)计算△ABC的面积;
(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com