
【题目】在△ABC中,AB=AC,点D为边BC上一点,且AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.
(1)求证:BE=CF;
(2)若∠B=40°,求∠ADF的度数.
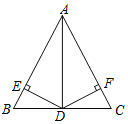
【答案】(1)见解析;(2)∠ADF=40°.
【解析】
(1)由角平分线的性质定理得出DE=DF,由等腰三角形的性质得出BD=CD,由HL证明Rt△BDE≌Rt△CDF,即可得出结论;
(2)由等腰三角形的性质和直角三角形的性质即可得出答案.
(1)证明:∵AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F.
∴DE=DF,∠DEB=∠DFC=90°,
∵AB=AC,AD平分∠BAC,
∴AD是BC边上的中线,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
![]() ,
,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF;
(2)∵AB=AC,
∴∠C=∠B=40°,
∵AB=AC,AD平分∠BAC,
∴AD⊥BC,
∴∠CAD=90°﹣40°=50°,
∴∠ADF=90°﹣∠CAD=40°.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】已知点A、B、C、D、E、F是半径为r的⊙O的六等分点,分别以A、D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
①∠PAD=∠PDA=60; ②△PAO≌△ADE;③PO=![]() r;④AO∶OP∶PA=1∶
r;④AO∶OP∶PA=1∶![]() ∶
∶![]() .
.
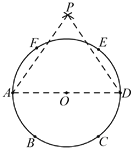
A. ①④B. ②③C. ③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
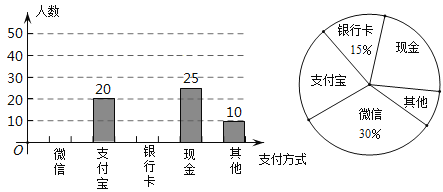
【题目】中国的数字支付正在引领未来世界的支付方式变革,中国消费者的移动支付比美国的移动支付要多出11倍,所以当我们展望数字钱包的未来时,中国是一个自然的起点.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种你最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)这次活动共调查了 人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为 ;
(2)将条形统计图补充完整.观察此图,将各种支付方式调查人数组成一组数据,求这组数据的“中位数”是“ ”;
(3)在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求两人选同种支付方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E是正方形内都一点,连接BE,CE,且∠ABE=∠BCE,点F是AB边上一动点,连接FD,FE,则FD+FE的长度最小值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
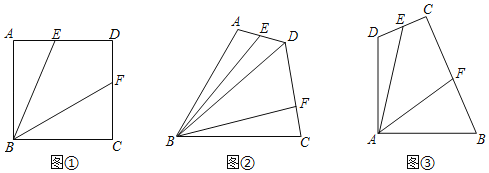
【题目】提出问题:(1)如图①,正方形ABCD中,点E,点F分别在边AD和边CD上,若正方形边长为4,DE+DF=4,则四边形BEDF的面积为 .
探究问题:(2)如图②,四边形ABCD,AB=BC=4,∠ABC=60°,∠ADC=120°,点E、F分别是边AD和边DC上的点,连接BE,BF,若ED+DF=3,BD=2![]() ,求四边形EBFD的面积;
,求四边形EBFD的面积;
解决问题:(3)某地质勘探队为了进行资源助测,建立了如图③所示的一个四边形野外勘查基地,基地相邻两侧边界DA、AB长度均为4km,∠DAB=90°,由于勘测需要及技术原因,主勘测仪C与基地边缘D、B夹角为90°(∠DCB=90°),在边界CD和边界BC上分别有两个辅助勘测仪E和F,辅助勘测仪E和F与主勘测仪C的距离之和始终等于4km(CE+CF=4).为了达到更好监测效果,需保证勘测区域(四边形EAFC)面积尽可能大.请问勘测区域面积有没有最大值,如果有求出最大值,如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
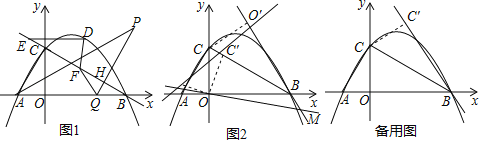
【题目】如图1,抛物线![]() 与y轴交于点C,与x轴交于点A、B(点A在点B左边),O为坐标原点.点D是直线BC上方抛物线上的一个动点,过点D作DE∥x轴交直线BC于点E.点P为∠CAB角平分线上的一动点,过点P作PQ⊥BC于点H,交x轴于点Q;点F是直线BC上的一个动点.
与y轴交于点C,与x轴交于点A、B(点A在点B左边),O为坐标原点.点D是直线BC上方抛物线上的一个动点,过点D作DE∥x轴交直线BC于点E.点P为∠CAB角平分线上的一动点,过点P作PQ⊥BC于点H,交x轴于点Q;点F是直线BC上的一个动点.
(1)当线段DE的长度最大时,求DF+FQ+![]() PQ的最小值.
PQ的最小值.
(2)如图2,将△BOC沿BC边所在直线翻折,得到△BOC′,点M为直线BO′上一动点,将△AOC绕点O顺时针旋转α度(0°<α<180°)得到△A′OC′,当直线A′C′,直线BO′,直线OM围成的图形是等腰直角三角形时,直接写出该等腰直角三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,tan∠CAD=![]() ,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
,CA=CD,E、F分别是AD、AC上的动点(点E与A、D不重合),且∠FEC=∠ACB.
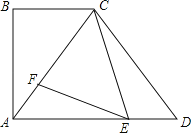
(1)求CD的长;
(2)若AF=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)当x为何值时,y>0?当x为何值时,y<0?
(3)写出y随x的增大而减小的自变量x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 两点,
两点,![]() 是直线
是直线![]() 上一动点,⊙
上一动点,⊙![]() 的半径为2.
的半径为2.
(1)判断原点![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)当⊙![]() 与
与![]() 轴相切时,求出切点的坐标.
轴相切时,求出切点的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com