
【题目】(1)(3分)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)(3分)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)(2分)把图(2)中的正方形都换成矩形,如图(3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

【答案】(1)HD:GC:EB=1:![]() :1(2)HD:GC:EB=1:
:1(2)HD:GC:EB=1: ![]() :1(3)有变化,HD:GC:EB=
:1(3)有变化,HD:GC:EB=![]()
【解析】解:(1)HD:GC:EB=1:![]() :1。
:1。
(2)连接AG、AC,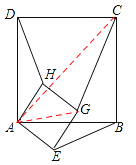
∵△ADC和△AHG都是等腰直角三角形,
∴AD:AC=AH:AG=1: ![]() ,∠DAC=∠HAG=45°。
,∠DAC=∠HAG=45°。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=1: ![]() 。
。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
又∵AD=AB,AH=AE,∴△DAH≌△BAE(SAS)。∴HD=EB。
∴HD:GC:EB=1: ![]() :1。
:1。
(3)有变化,HD:GC:EB=![]() 。
。
(1)连接AG,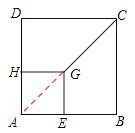
∵正方形AEGH的顶点E、H在正方形ABCD的边上,
∴∠GAE=∠CAB=45°,AE=AH,AB=AD。
∴A,G,C共线,AB-AE=AD-AH,∴HD=BE。
∵![]()
∴GC=AC-AG=![]() AB-
AB-![]() AE=
AE= ![]() (AB-AE)=
(AB-AE)= ![]() BE。
BE。
∴HD:GC:EB=1:![]() :1。
:1。
(2)连接AG、AC,由△ADC和△AHG都是等腰直角三角形,易证得△DAH∽△CAG与△DAH≌△BAE,利用相似三角形的对应边成比例与正方形的性质,即可求得HD:GC:EB的值。
(3)连接AG、AC,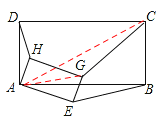
∵矩形AEGH的顶点E、H在矩形ABCD的边上,
DA:AB=HA:AE=m:n,
∴∠ADC=∠AHG=90°,∴△ADC∽△AHG。
∴AD:AC=AH:AG=![]() ,∠DAC=∠HAG。
,∠DAC=∠HAG。
∴∠DAH=∠CAG。∴△DAH∽△CAG。
∴HD:GC=AD:AC=![]() 。
。
∵∠DAB=∠HAE=90°,∴∠DAH=∠BAE。
∵DA:AB=HA:AE=m:n,∴△ADH∽△ABE。∴DH:BE=AD:AB=m:n。
∴HD:GC:EB=![]() 。
。


科目:初中数学 来源: 题型:
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,已知点![]() 的坐标
的坐标![]() ,点
,点![]() 位置如图所示,点
位置如图所示,点![]() 与点
与点![]() 关于原点对称。
关于原点对称。
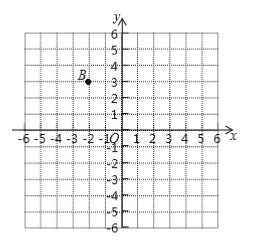
(1)在图中描出点![]() ;写出图中点
;写出图中点![]() 的坐标:______________,点
的坐标:______________,点![]() 的坐标:_______________;
的坐标:_______________;
(2)画出![]() 关于
关于![]() 轴的对称图形
轴的对称图形![]() ,并求出四边形
,并求出四边形![]() 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
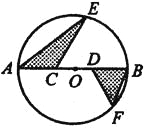
【题目】如图,半径为6cm 的⊙O中,C,D为直径AB 的三等分点,点E,F分别在AB两侧的半圆上,∠BCE =∠BDF = 60°,连结AE,BF.则图中两个阴影部分的面积和为 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进枇杷20吨,桃子12吨.现计划租用甲、乙两种货车共8辆将这批水果运回,已知一辆甲种货车可装枇杷4吨和桃子1吨,一辆乙种货车可装枇杷和桃子各2吨.
(1)如何安排甲、乙两种货车可一次性地运到?有几种方案?
(2)若甲种货车每辆要付运输费300元,乙种货车每辆要付运输费240元,则果商场应选择哪种方案,使运输费最少?最少运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
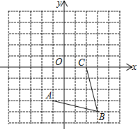
【题目】如图,在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度
(1) 请在所给的网格内画出以线段AB、BC为边的□ABCD并写出点D的坐标_________
(2) 线段BD的长为_____________
(3) 点C到AB的距离为_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com