
【题目】如图,等腰Rt△ABP的斜边AB=2,点M、N在斜边AB上.若△PMN是等腰三角形且底角正切值为2,则MN=_________.

【答案】1或![]()
【解析】
分MN是底边与MP是底边,分别作图,根据等腰三角形的性质及正切的定义即可求解.
如图,当MN是底边的等腰△PMN时
作PH⊥AB,∵△PAB是等腰直角三角形,
∴PH=AH=BH=![]() AB=1
AB=1
∵△PMN是等腰三角形且底角正切值为2,
故tan∠PMN=2
即![]()
解得MH=![]()
∴MN=2MH=1;
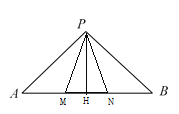
如图,当MP是底边的等腰△PMN时,
作PH⊥AB,∵△PAB是等腰直角三角形,
∴PH=AH=BH=![]() AB=1
AB=1
∵△PMN是等腰三角形且底角正切值为2,
故tan∠PMN=2
∴MH=![]()
设PN=MN=x,则HN=x-![]()
∵PN2=PH2+HN2
即x2=12+( x-![]() )2
)2
解得x=![]() ,
,
综上,MN=1或![]()
故答案为:1或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )

A.∠A=60°B.△ACD是直角三角形
C.BC=![]() CDD.点B是△ACD的外心
CDD.点B是△ACD的外心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教育行政部门为了了解初一学生每学期参加综合实践活动的情况,随机抽样调查了某校初一学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).
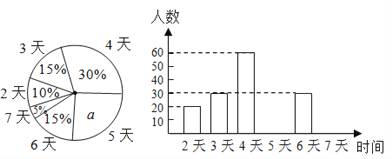
请你根据图中提供的信息,回答下列问题:
(1)求出扇形统计图中a的值,并求出该校初一学生总数;
(2)分别求出活动时间为5天、7天的学生人数,并补全频数分布直方图;
(3)求出扇形统计图中“活动时间为4天”的扇形所对圆心角的度数;
(4)在这次抽样调查中,众数和中位数分别是多少?
(5)如果该市共有初一学生6000人,请你估计“活动时间不少于4天”的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2,AD=![]() ,E是CD边上的中点,P是BC边上的一点,且BP=2CP,连接EP并延长交AB的延长线于点F.
,E是CD边上的中点,P是BC边上的一点,且BP=2CP,连接EP并延长交AB的延长线于点F.
(1)求BF;
(2)判断EB是否平分∠AEC,并说明理由;
(3)连接AP,不添加辅助线,试证明△AEP≌△FBP,直接写出一种经过两次变换的方法使得△AEP与△FBP重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2020盐城国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小华参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 ;
(2)请用表格或树状图列出所有可能情况,求小明和小华被分配到不同项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c的对称轴是x=![]() ,小亮通过观察得出了下面四条信息:①
,小亮通过观察得出了下面四条信息:①![]() ,②abc<0,③4a+2b+c>0,④2a+3b=0.你认为其中正确的有_________________.
,②abc<0,③4a+2b+c>0,④2a+3b=0.你认为其中正确的有_________________.
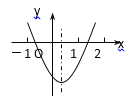
A.①②B.②④C.①③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做好开学准备,某校共购买了20桶A、B两种桶装消毒液,进行校园消杀,以备开学.已知A种消毒液300元/桶,每桶可供2 000米2的面积进行消杀,B种消毒液200元/桶,每桶可供1 000米2的面积进行消杀.
(1)设购买了A种消毒液x桶,购买消毒液的费用为y元,写出y与x之间的关系式,并指出自变量x的取值范围;
(2)在现有资金不超过5 300元的情况下,求可消杀的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了考查学生的综合素质,某市决定:九年级毕业生统一参加中考实验操作考试,根据今年的实际情况,中考实验操作考试科目为:![]() (物理)、
(物理)、![]() (化学)、
(化学)、![]() (生物),每科试题各为
(生物),每科试题各为![]() 道,考生随机抽取其中
道,考生随机抽取其中![]() 道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
道进行考试.小明和小丽是某校九年级学生,需参加实验考试.
(1)小明抽到化学实验的概率为 ;
(2)若只从考试科目考虑,小明和小丽抽到不同科目的概率为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com