

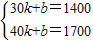 ,
, ,
, ,
,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
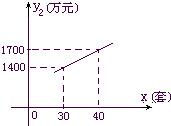 间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.
间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图所示的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:
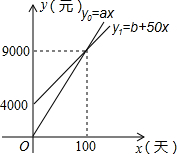 (2012•泉州)国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时x(单位:天)之间分别满足关系式:y0=ax、y1=b+50x,如图所示.
(2012•泉州)国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时x(单位:天)之间分别满足关系式:y0=ax、y1=b+50x,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
| 月份x | 7月 | 8月 | 9月 | 10月 | … |
| 售价 y(元/个) | 56 | 60 | 64 | 68 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
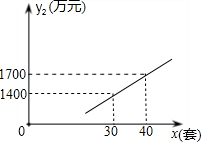 合适?
合适?查看答案和解析>>
科目:初中数学 来源: 题型:
 国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时x(单位:天)之间分别满足关系式:y0=ax、y1=b+50x,如图所示.
国家推行“节能减排,低碳经济”政策后,某企业推出一种叫“CNG”的改烧汽油为天然气的装置,每辆车改装费为b元,据市场调查知:每辆车改装前、后的燃料费(含改装费)y0、y1(单位:元)与正常运营时x(单位:天)之间分别满足关系式:y0=ax、y1=b+50x,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com