
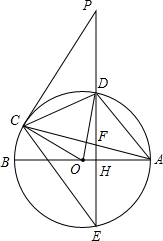
 如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F,P是延长线上一点,且PC=PF.
如图,AB、AC分别是⊙O的直径和弦,点D为劣弧AC上一点,弦DE⊥AB分别交⊙O于点D、E,交AB于点H,交AC于点F,P是延长线上一点,且PC=PF.分析 (1)根据等腰三角形的性质和直角三角形两锐角互余的性质,证得∠PCF+∠AC0=90°,即OC⊥PC,即可证得结论;
(2)乘积的形式通常可以转化为比例的形式,通过证明三角形相似得出.
(3)首先求出DF、DE,再根据PC2=PD•PE,即(PD+DF)2=PD(PD+DE)计算即可.
解答 (1)证明:∵OA=OC,
∴∠ACO=∠OAC,
∵PC=PF,
∴∠PCF=∠PFC,
∵DE⊥AB,
∴∠OAC+∠AFH=90°,
∵∠PDF=∠AFH,
∴∠PFC+∠OAC=90°,
∴∠PCF+∠AC0=90°,
即OC⊥PC,
∴PC是⊙O的切线;
(2)连接AE.
∵AD2=DE•DF,
∴AD:ED=FD:AD,
∵∠ADF=∠ADE,
∴△DAF∽△DEA,
∴∠DAF=∠DEA,
∴点D是劣弧AC的中点,
∵DE⊥AB,
∴$\widehat{AD}$=$\widehat{AE}$,
∴$\widehat{CD}$=$\widehat{AE}$,
∴∠ACE=∠DEC,
∴CF=EF;
(3)解:由(2)可知:AD=CD,∠ACD=∠CAD.
∵∠PCD=∠CAD,
∵OH=1,AH=2,
∴OD=3,DH=2√2,DE=2DH=4√2,AD=2√3,
∵AD2=DE•DF⇒(2√3)2=4√2×DF.
∴DF=3√2/2,
∵PC=PF,PC2=PD•PE⇒PF2=PD•PE,
∴(PD+DF)2=PD(PD+DE),
∴2PD×(3√2/2)+(3√2/2)2=PD×4√2,
∴PD=9√2/4,
∴PC2=PD(PD+DE)=(9√2/4)2+(9√2/4)×4√2,
∴PC=$\frac{15\sqrt{2}}{4}$.
点评 本题考查了切线的判定、全等三角形的判定和性质、相似三角形的判定和性质、切割线定理、垂径定理等知识,解题的关键是灵活运用这些知识,寻找相似三角形是突破点,属于中考常考题型.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{4}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{4}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com