
 低碳经济作为新的发展模式,不仅是实现全球减排目标的战略选择,也是保证经济持续健康增长的良方.中国企业目前已经在多个低碳产品和服务领域取得世界领先地位,其中以可再生资源相关行业最为突出.某单位为了发展低碳经济,采取技术革新,让可再生产资源重新利用.从2011年1月1日开始,该单位每月再生资源处理量y(吨)与月份x之间成一次函数关系,如图所示.月处理成本p(元)与每月再生资源y(吨)满足的函数关系p=10y2-400y+14000.每处理一吨再生资源得到的新产品的售价定为2000元.
低碳经济作为新的发展模式,不仅是实现全球减排目标的战略选择,也是保证经济持续健康增长的良方.中国企业目前已经在多个低碳产品和服务领域取得世界领先地位,其中以可再生资源相关行业最为突出.某单位为了发展低碳经济,采取技术革新,让可再生产资源重新利用.从2011年1月1日开始,该单位每月再生资源处理量y(吨)与月份x之间成一次函数关系,如图所示.月处理成本p(元)与每月再生资源y(吨)满足的函数关系p=10y2-400y+14000.每处理一吨再生资源得到的新产品的售价定为2000元.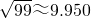 ,
,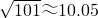 ,
,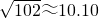 )
) ,
,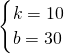 ,
,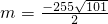 ,
,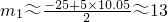 ,
,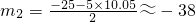 (舍去).
(舍去).

科目:初中数学 来源: 题型:
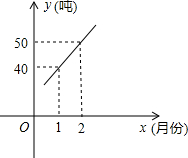 低碳经济作为新的发展模式,不仅是实现全球减排目标的战略选择,也是保证经济持续健康增长的良方.中国企业目前已经在多个低碳产品和服务领域取得世界领先地位,其中以可再生资源相关行业最为突出.某单位为了发展低碳经济,采取技术革新,让可再生产资源重新利用.从2011年1月1日开始,该单位每月再生资源处理量y(吨)与月份x之间成一次函数关系,如图所示.月处理成本p(元)与每月再生资源y(吨)满足的函数关系p=10y2-400y+14000.每处理一吨再生资源得到的新产品的售价定为2000元.
低碳经济作为新的发展模式,不仅是实现全球减排目标的战略选择,也是保证经济持续健康增长的良方.中国企业目前已经在多个低碳产品和服务领域取得世界领先地位,其中以可再生资源相关行业最为突出.某单位为了发展低碳经济,采取技术革新,让可再生产资源重新利用.从2011年1月1日开始,该单位每月再生资源处理量y(吨)与月份x之间成一次函数关系,如图所示.月处理成本p(元)与每月再生资源y(吨)满足的函数关系p=10y2-400y+14000.每处理一吨再生资源得到的新产品的售价定为2000元.| 99 |
| 101 |
| 102 |
查看答案和解析>>
科目:初中数学 来源:2011年重庆市沙坪坝区中考数学模拟试卷(三)(解析版) 题型:解答题
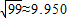 ,
, ,
,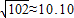 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com