
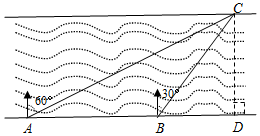
 如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,
如图,在与南渡江对岸平行的岸边有A、B、D三点,A、B、D三点在同一直线上,在A点处测得河对岸C点在北偏东60°方向;从A点沿河边前进200米到达B点,这时测得C点在北偏东30°方向,分析 (1)在Rt△ACD中,求出∠CAD即可解决问题;
(2)首先由题意可得:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,AB=200米,CD⊥AB,则可证得△ABC是等腰三角形,即BC=AB,然后在Rt△CBD中,由CD=BC•sin60°,即可求得答案.
解答 解:(1)作CD⊥AB于D.
∵在A点处测得河对岸C点在北偏东60°方向,
∴∠CAD=30°,
∵∠ADC=90°,
∴∠ACD=90°-30°=60°.
(2)根据题意得:∠CAB=90°-60°=30°,∠CBD=90°-30°=60°,AB=200米,CD⊥AB,
则∠ACB=∠CBD-∠CAB=60°-30°=30°,
则BC=AB=200米,
在Rt△CBD中,CD=BC•sin60°=200×$\frac{\sqrt{3}}{2}$=100 $\sqrt{3}$(米).
答:河宽CD为100 $\sqrt{3}$米.
点评 此题考查了方向角问题.此题难度适中,注意能借助于解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
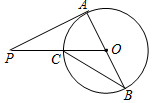 如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )
如图,AB是⊙O的直径,PA切⊙O于点A,PO交⊙O于点C,连结BC.若∠P=18°,则∠B等于( )| A. | 27° | B. | 30° | C. | 36° | D. | 54°图3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2条 | B. | 3条 | C. | 4条 | D. | 无数条 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com