
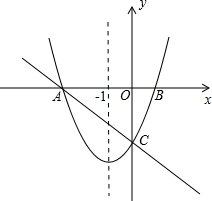
 ��ͼ����ֱ������ϵxOy�У�һ�κ���y=-$\frac{2}{3}$x+m��mΪ��������ͼ����x�ύ��A��-3��0������y�ύ�ڵ�C����ֱ��x=-1Ϊ�Գ����������y=ax+bx+c��a��b��cΪ��������a��0������A��C���㣬��x�������ύ�ڵ�B��
��ͼ����ֱ������ϵxOy�У�һ�κ���y=-$\frac{2}{3}$x+m��mΪ��������ͼ����x�ύ��A��-3��0������y�ύ�ڵ�C����ֱ��x=-1Ϊ�Գ����������y=ax+bx+c��a��b��cΪ��������a��0������A��C���㣬��x�������ύ�ڵ�B������ ��1�����ݴ���ϵ��������ֱ�����һ�κ�������ʽ������A������ͶԳ������B�����꣬���ý���ʽ����������κ�������ʽ��
��2��Ҫʹ��PBC���ܳ���С��ֻ��BP+CP��С���ɣ����ֱ��AC����ʽ����x=-1���뼴�����P�������꣬�Ӷ����P�����ꣻ
��3����S��PDEת��ΪS��AOC-S��DOE-S��PDC-S��PEA����ת��Ϊ����x�Ķ��κ�����Ȼ������κ��������ֵ��
��� �⣺��1����y=-$\frac{2}{3}$x+m������A��-3��0����
��0=2+m�����m=-2��
��ֱ��AC����ʽΪy=-$\frac{2}{3}$x-2��
C��0��-2����
��������y=ax2+bx+c�Գ���Ϊx=-1������x�ύ��A��-3��0����
����һ����ΪB��1��0�����������߽���ʽΪy=a��x+3����x-1����
�������߾��� C��0��-2����
��-2=a•3��-1�������a=$\frac{2}{3}$��
�������߽���ʽΪy=$\frac{2}{3}$x2+$\frac{4}{3}$x-2��
��2��Ҫʹ��PBC���ܳ���С��ֻ��BP+CP��С���ɣ���ͼ1��
����AC��x=-1��P�㣬��Ϊ��A��B����x=-1�Գƣ�������Գ������Լ�����֮���߶���̣���֪��ʱBP+CP��С��BP+CP��СֵΪ�߶�AC�ij��ȣ���
��A��-3��0������0����C��0��-2����
��ֱ��AC����ʽΪy=-$\frac{2}{3}$x-2��
��xP=-1��
��yP=-$\frac{4}{3}$����P��-1��-$\frac{4}{3}$��
��3����ͼ2��
����CD�ij�Ϊm����PDE�����ΪS��
��D��0��m-2����
��DE��PC��ֱ��AC����ʽΪy=-$\frac{2}{3}$x-2��
����ֱ��DE����ʽy=-$\frac{2}{3}$x+m-2��
��y=0ʱ��x=$\frac{3}{2}$m-3��
��E��$\frac{3}{2}$m-3��0����
S��PDE=S��AOC-S��DOE-S��PDC-S��PEA
=3-$\frac{1}{2}$��$\frac{3}{2}$m��$\frac{4}{3}$-$\frac{1}{2}$����3-$\frac{3}{2}$m������2-m��-$\frac{1}{2}$��m��1
=-$\frac{3}{4}$m2+$\frac{3}{2}$m
=-$\frac{3}{4}$��m-1��2+$\frac{3}{4}$��
�൱m=1ʱ�����ֵ$\frac{3}{4}$��
���� ���⿼���˶��κ����ۺ��⣬�漰����ϵ��������κ�����ʽ����Գ����·�����⡢�����ε������ʽ�����κ��������ֵ���ۺ��Խ�ǿ����1�����ݶԳ������B�������ǽ���Ĺؼ�����2���У�Ҫ��Ϥ��ԳƵ����ʣ���3��Ҫ��Ϥ���κ�������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
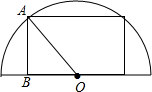 ��һ���ִ�װ�������ˮ���ϻ����6m����4.4�ף�����ͨ��һ��ֱ��10m�İ�Բ�ι�����
��һ���ִ�װ�������ˮ���ϻ����6m����4.4�ף�����ͨ��һ��ֱ��10m�İ�Բ�ι������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
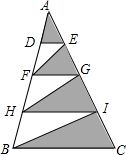 ��ͼ��������ABC�У���AB��AC�ֱ��ĵȷ֣���֪������ADE�������6cm2������Ӱ���ֵ������
��ͼ��������ABC�У���AB��AC�ֱ��ĵȷ֣���֪������ADE�������6cm2������Ӱ���ֵ�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
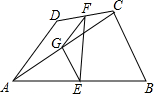 ��ͼ�����ı���ABCD�У�AD=BC��E��F��G�ֱ���AB��CD��AC���е㣬����DAC=36�㣬��ACB=84�㣬���FEG���ڣ�������
��ͼ�����ı���ABCD�У�AD=BC��E��F��G�ֱ���AB��CD��AC���е㣬����DAC=36�㣬��ACB=84�㣬���FEG���ڣ�������| A�� | 20�� | B�� | 24�� | C�� | 26�� | D�� | 15�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 1 | C�� | -12 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m | B�� | -m | C�� | 3m | D�� | -3m |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾΪij������ʻ��·��S��km����ʱ��t��min���ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ����������⣺
��ͼ��ʾΪij������ʻ��·��S��km����ʱ��t��min���ĺ�����ϵͼ���۲�ͼ�����ṩ����Ϣ����������⣺�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com