
分析 观察数的规律可知,每一项都是分数,且分子为1,分母为该数的序号与比该数的序号多1的数的积,即第n个数为$\frac{1}{(n+1)(n+2)}$(n≥1).
解答 解:第1个数:$\frac{1}{6}$=$\frac{1}{2×3}$;
第2个数:$\frac{1}{12}$=$\frac{1}{3×4}$;
第3个数:$\frac{1}{20}$=$\frac{1}{4×5}$,
…
第n个数:$\frac{1}{(n+1)(n+2)}$,
所以第99个数是:$\frac{1}{100×101}$=$\frac{1}{10100}$.
故答案是:$\frac{1}{10100}$.
点评 本题考查了数字的变化规律及有理数的加法运算.关键是找出分母中的数与序号的关系.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
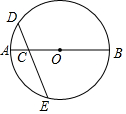 如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若$\widehat{AD}$的度数为35°,求$\widehat{BE}$的度数.
如图,C是⊙O的直径AB上一点,过点C作弦DE,使CD=CO,若$\widehat{AD}$的度数为35°,求$\widehat{BE}$的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com