
 如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.(1)BE=CF,(2)AC=DF,(3)∠ABC=∠DEF,(4)AB=DE.
如图,在△ABC和△DEF中,B、E、C、F在同一直线上,下面有四个条件,请你在其中选3个作为条件,余下的1个作为结论,使其成为一个真命题,并加以证明.(1)BE=CF,(2)AC=DF,(3)∠ABC=∠DEF,(4)AB=DE.分析 选择的条件(1)(2)(4)或(1)(3)(4),分别利用SSS或SAS判定三角形全等.
解答 解:我所选择的条件是:(1)(2)(4)
∵BE=CF,
∴BC=EF,
在△ABC和△DEF中,
$\left\{\begin{array}{l}{AB=DE}\\{BC=EF}\\{AC=DF}\end{array}\right.$
∴△ABC≌△DEF,
∴∠ABC=∠DEF.
(如果选1,3,4.可以利用SAS证明三角形全等).
故答案分别为BE=CF、AC=DF、AB=DE或BE=CF,∠ABC=∠DEF,AB=DE,∠ABC=∠DEF或AC=DF;省略.
点评 本题考查命题与定理、全等三角形的判定和性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:解答题
 已知:如图,在梯形ABCD中,上底AD=$\sqrt{12}$,下底BC=$\sqrt{48}$,高AE=$\sqrt{27}$,求梯形ABCD的面积.
已知:如图,在梯形ABCD中,上底AD=$\sqrt{12}$,下底BC=$\sqrt{48}$,高AE=$\sqrt{27}$,求梯形ABCD的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),请你分别完成下面的作图并标出所有顶点的坐标.
△ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),请你分别完成下面的作图并标出所有顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
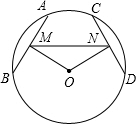 如图,AB、CD是⊙O的弦,OM⊥AB,ON⊥CD,垂足分别为M、N,且∠AMN=∠CNM.
如图,AB、CD是⊙O的弦,OM⊥AB,ON⊥CD,垂足分别为M、N,且∠AMN=∠CNM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.
平面直角坐标系中,矩形OABC放置如图,点A(3,0)、C(0,9),现将它绕点B逆时针旋转得矩形O′A′BC′,点O的对应点O′在x轴上,O′C′交AB于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 有一个内角为45°的直角三角形 | ||
| C. | 直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com