解：（1）∵直线y=2x与某反比例函数图象的一个交点的横坐标为2，
∴这个交点的纵坐标为：2×2=4，
设反比例函数的解析式为y=
，
∴k=xy=2×4=8，
∴y=
；
（2）作出反比例函数的图象，如图；
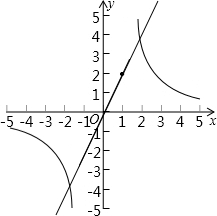
（3）相似处：两个函数都经过一三象限；都经过（2，4），（-2，-4）两点；
不同点：正比例函数与坐标轴有交点，反比例函数与坐标轴无交点；
正比例函数的图象是一条直线，反比例函数的图象是双曲线；
正比例函数的自变量的取值为全体实数，反比例函数自变量不能取x=0；
（4）当0＜x＜2时，两个函数值均为非负数且反比例函数大于正比例函数值．
分析：（1）把点的横坐标代入直线解析式可求得点的纵坐标，把所得点的横纵坐标代入反比例函数解析式可求得比例系数；
（2）直线解析式经过点（2，4）及原点；反比例函数应从自变量为正值和负值各取几个数得到相应的图象；
（3）根据所在象限得到相似处，经过原点与否得到不同处；
根据都经过某两点得到相似处，根据图象的不同以及自变量的取值得到不同处；
（4）找到x轴上方y轴右侧相同的自变量，反比例函数的函数值大于正比例函数的函数值所对应的自变量的取值范围即可．
点评：反比例函数的比例系数等于在它上面的点的横纵坐标的积；看相同自变量所对应的函数值不同应从两个函数交点入手思考；注意从不同方面找到两个函数的相似处和不同处．
