
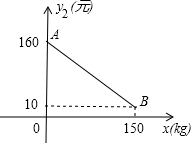
 某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足关系式y1=$\left\{\begin{array}{l}{-0.5x+100(0≤x<80)}\\{3x-180(80≤x≤150)}\end{array}\right.$.如图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数关系式.
某加工企业生产并销售某种农产品,假设销售量与加工产量相等.已知每千克生产成本y1(单位:元)与产量x(单位:kg)之间满足关系式y1=$\left\{\begin{array}{l}{-0.5x+100(0≤x<80)}\\{3x-180(80≤x≤150)}\end{array}\right.$.如图中线段AB表示每千克销售价格y2(单位:元)与产量x(单位:kg)之间的函数关系式.分析 (1)待定系数法求解可得;
(2)根据总利润=(每千克销售价格-每千克生产成本)×产量,分0≤x<80和80≤x≤150两种情况,分别列式可得;
(3)将x=70代入(2)中相应函数解析式可得.
解答 解:(1)设y2=kx+b,
将点A(0,160)、B(150,10)代入,得:
$\left\{\begin{array}{l}{b=160}\\{150k+b=10}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=160}\end{array}\right.$,
∴y2=-x+160(0≤x≤150);
(2)根据题意,当0≤x<80时,w=[-x+160-(-0.5x+100)]•x=-0.5x2+60x,
当80≤x≤150时,w=[-x+160-(3x-180)]•x=-4x2+340x;
(3)∵当x=70时,w=-0.5×702+60×70=1750>0,
∴销售量为70kg时,销售该农产品是盈利的,盈利1750元.
点评 本题主要考查待定系数法求函数解析式及二次函数的应用,理清题意找到题目蕴含的相等关系是解题的关键.


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com