
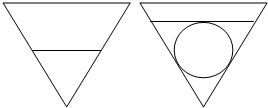
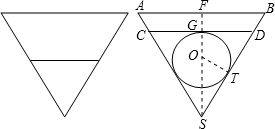
 如图:有一轴截面为正三角形的圆锥形容器,内部盛水高度为10cm,放入一个球后,水面恰好与球相切,求球的半径.(圆锥的体积公式V=
如图:有一轴截面为正三角形的圆锥形容器,内部盛水高度为10cm,放入一个球后,水面恰好与球相切,求球的半径.(圆锥的体积公式V=| 1 |
| 3 |
| 4 |
| 3 |
| ||
| 3 |
10
| ||
| 3 |
| π |
| 3 |
| π |
| 9 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 3 |
| 4π |
| 3 |
| 4 |
| 3 |
| π |
| 9 |
| |||
| 15 |
2
| |||
| 3 |
2
| |||
| 3 |


科目:初中数学 来源: 题型:
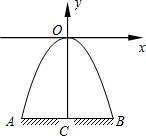 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
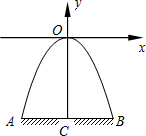 如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:
如图,某隧道口的横截面是抛物线形,已知路宽AB为6米,最高点离地面的距离OC为5米.以最高点O为坐标原点,抛物线的对称轴为y轴,1米为数轴的单位长度,建立平面直角坐标系.求:查看答案和解析>>
科目:初中数学 来源:2012届九年级第二学期第一阶段考试数学卷(解析版) 题型:解答题
如图,隧道的截面由抛物线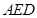 和矩形
和矩形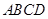 构成,矩形的长
构成,矩形的长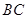 为
为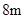 ,宽
,宽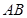 为
为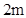 ,以
,以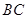 所在的直线为
所在的直线为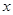 轴,线段
轴,线段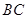 的中垂线为
的中垂线为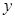 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,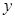 轴是抛物线的对称轴,顶点
轴是抛物线的对称轴,顶点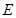 到坐标原点
到坐标原点 的距离为
的距离为 .
.
(1)求抛物线的解析式;
 (2)一辆货运卡车高
(2)一辆货运卡车高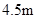 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设
有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
查看答案和解析>>
科目:初中数学 来源:2012届九年级第二学期第一阶段考试数学卷(解析版) 题型:解答题
如图,隧道的截面由抛物线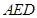 和矩形
和矩形 构成,矩形的长
构成,矩形的长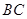 为
为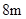 ,宽
,宽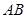 为
为 ,以
,以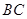 所在的直线为
所在的直线为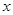 轴,线段
轴,线段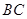 的中垂线为
的中垂线为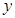 轴,建立平面直角坐标系,
轴,建立平面直角坐标系,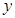 轴是抛物线的对称轴,顶点
轴是抛物线的对称轴,顶点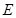 到坐标原点
到坐标原点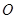 的距离为
的距离为 .
.
(1)求抛物线的解析式;
 (2)一辆货运卡车高
(2)一辆货运卡车高 ,宽2.4m,它能通过该隧道吗?
,宽2.4m,它能通过该隧道吗?
(3)如果该隧道内设双行道,为了安全起见,在隧道正中间设
有0.4m的隔离带,则该辆货运卡车还能通过隧道吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com