
| A. | a(x1-x2)=d | B. | a(x2-x1)=d | C. | a(x1-x2)2=d | D. | a(x1+x2)2=d |
分析 由x=x1是方程a(x-x1)(x-x2)=0和dx+e=0的一个公共解,可得出x=x1是方程a(x-x1)(x-x2)+dx+e=0的一个解,根据根与系数的关系即可得出x1+x1=-$\frac{-(a{x}_{1}+a{x}_{2}-d)}{a}$,整理后即可得出结论.
解答 解:∵关于x的一元二次方程a(x-x1)(x-x2)=0与关于x的一元一次方程dx+e=0有一个公共解x=x1,
∵x=x1是方程a(x-x1)(x-x2)+dx+e=0的一个解.
∵方程a(x-x1)(x-x2)+dx+e=ax2-(ax1+ax2-d)x+ax1•x2+e=0只有一个解,
∴x1+x1=-$\frac{-(a{x}_{1}+a{x}_{2}-d)}{a}$,
整理得:d=a(x2-x1).
故选B.
点评 本题考查了一元二次方程的解以及根与系数的关系,根据根与系数的关系找出x1+x1=-$\frac{-(a{x}_{1}+a{x}_{2}-d)}{a}$是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AE⊥AB交BC于点E.若S△ABC=m2+9n2,S△ADE=mn,则m与n之间的数量关系是( )
如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AE⊥AB交BC于点E.若S△ABC=m2+9n2,S△ADE=mn,则m与n之间的数量关系是( )| A. | m=3n | B. | m=6n | C. | n=3m | D. | n=6m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:| x(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
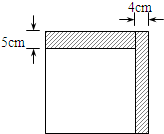 如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )
如图,小明将一个正方形纸剪出一个宽为4cm的长条后,再从剩下的长方形纸片上剪去一个宽为5cm的长条,如果两次剪下的长条面积正好相等,那么每一个长条面积为( )| A. | 16cm2 | B. | 20cm2 | C. | 80cm2 | D. | 160cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com