
| x | 35 | 40 | 45 | 50 |
| y | 57 | 42 | 27 | 12 |
分析 (1)根据待定系数法求解可得;
(2)根据“总利润=单件利润×销售量”得到函数解析式,配方成顶点式即可得其最大值.
解答 解:(1)因日销售量y件与销售价x元满足一次函数,
故一次函数设为:y=ax+b,
由题意得:
$\left\{\begin{array}{l}{45a+b=27}\\{50a+b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-3}\\{b=162}\end{array}\right.$,
故y=162-3x为所求的函数关系式,
∵y≥0,
∴0≤x≤54.
?(2)依题意得:P=(x-30)•y=(x-30)•(162-3x)=-3(x-42)2+432.
当x=42时,ymax=432,
即销售单价为42元/件时,获最大日销售利润432元.
答:当销售单价x为42元时,才能获得最大的销售利润.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法和依据相等关系列出函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 重量(千克) 费用(元) | 0.5 | 1 | 3 | 4 | … |
| 甲公司 | 11 | 22 | 52 | 67 | … |
| 乙公司 | 11 | 19 | 51 | 67 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
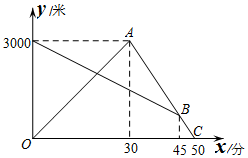 某天早晨,小刚从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,小刚跑到体育场后发现要下雨,立即以另一速度按原路返回,遇到妈妈后,妈妈立即以小刚返回的速度和小刚一起回家(妈妈与小刚行进的路线相同).如图是两人离家的距离y(米)与小刚出发的时间x(分)之间的函数图象,则小刚第一次和妈妈相遇时,妈妈离家的距离为2000 米.
某天早晨,小刚从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,小刚跑到体育场后发现要下雨,立即以另一速度按原路返回,遇到妈妈后,妈妈立即以小刚返回的速度和小刚一起回家(妈妈与小刚行进的路线相同).如图是两人离家的距离y(米)与小刚出发的时间x(分)之间的函数图象,则小刚第一次和妈妈相遇时,妈妈离家的距离为2000 米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com