
【题目】如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B.
(1)求证:点C是劣弧![]() 的中点;
的中点;
(2)如图②,连结EC,若AE=2AC=6,求阴影部分的面积.
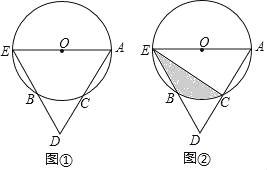
【答案】(1)证明见解析;(2)![]() ;
;
【解析】
(1)连接CE,由AE是⊙O的直径,得到CE⊥AD,根据等腰三角形的性质得到∠AEC=∠DEC,于是得到结论;
(2)连接BC,OB,OC,由已知条件得到△AED是等边三角形,得到∠A=60°,推出AE∥BC,∠BOC=60°,于是得到结论.
(1)连接CE,
∵AE是⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴AE=ED,
∴∠AEC=∠DEC,
∴![]() ;
;
∴点C是劣弧![]() 的中点;
的中点;
(2)连接BC,OB,OC,
∵AE=2AC=6,
∴∠AEC=30°,AE=AD,
∴∠AED=60°,
∴△AED是等边三角形,
∴∠A=60°,
∵![]() ,
,
∴![]() ,
,
∴AE∥BC,∠BOC=60°,
∴S△OBC=S△EBC,
∴S阴影=S扇形=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
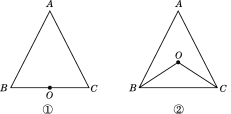
(1)如图①,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图②,若点O在△ABC内部,求证AB=AC.
(3)若点O在△ABC的外部,AB=AC还成立吗?请画图说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
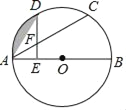
【题目】如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.
(1)求证:AF=DF.
(2)求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD是△ABC的中线,AE∥BC,射线BE交AD于点F,交⊙O于点G,点F是BE的中点,连接CE.
(1)求证:四边形ADCE为平行四边形;
(2)若BC=2AB,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进“足球进校园”活动的开展,某市举行了中学生足球比赛活动现从A,B,C三支获胜足球队中,随机抽取两支球队分别到两所边远地区学校进行交流.
(1)请用列表或画树状图的方法(只选择其中一种),表示出抽到的两支球队的所有可能结果;
(2)求出抽到B队和C队参加交流活动的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com