
【题目】如图,已知在平面直角坐标系中,四边形ABCD是长方形,∠A=∠B=∠C=∠D=90°,AB∥CD,AB=CD=8cm,AD=BC=6cm,D点与原点重合,坐标为(0,0)
(1)写出点B的坐标;
(2)动点P从点A出发以每秒3个单位长度的速度向终点B匀速运动,动点Q从点C出发以每秒4个单位长度的速度沿射线CD方向匀速运动,若P,Q两点同时出发,设运动时间为t,当t为何值时,PQ∥BC;
(3)在Q的运行过程中,当Q运动到什么位置时,使△ADQ的面积为9,求此时Q点的坐标.

【答案】(1)B(8,6)(2)t为![]() (3)当Q运动到距原点3cm位置时,使△ADQ的面积为9,此时Q点的坐标(3,0)或(-3,0)
(3)当Q运动到距原点3cm位置时,使△ADQ的面积为9,此时Q点的坐标(3,0)或(-3,0)
【解析】
试题(1)根据点的特点可以直接写出坐标;
(2)由平行的位置和移动的距离可以设出时间t,从而构成方程解决;
(3)分在D点左右两边两种情况讨论构成的三角形,根据面积求出点的坐标.
试题解析:(1)∵AB=DC=8 AD=BC=6
∴B(8,6)
(2)运动时间为t秒 则t秒时P(3t,6)Q(8-4t,0)
∵PQ ∥BC 且 BC∥ AO
∴PQ∥A0即y轴
∴ 3t=8-4t
∴t=![]()
∴t=![]() 秒时 PQ//BC
秒时 PQ//BC
(3)∵Q在射线CD方向匀速运动.
Q在0点右侧时Q坐标(8-4t,0)
S=![]() AD.DQ
AD.DQ
∴9=![]() ×6(8-4t)
×6(8-4t)
∴t=![]()
此时8-4t=8-4×![]() =3
=3
∴Q(3,0)
Q在点0左侧时Q(8-4t,0) S=![]() AD×DQ 9=
AD×DQ 9=![]() ×6×(4t-8)
×6×(4t-8)
∴t=![]()
此时8-4t=8-4×![]() =-3
=-3
∴Q(-3,0)
∴Q点距原点3个单位时,面积为9
此时Q(3,0)或(-3,0)


 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4,E是BC上一点,将△CDE沿直线DE折叠后,点C落在点C′处,连接C′E交AD于点F,若BE=2,F为AD的中点,则AD的长为 . 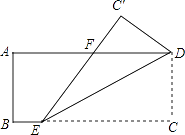
查看答案和解析>>
科目:初中数学 来源: 题型:
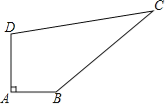
【题目】如图,某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
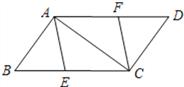
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
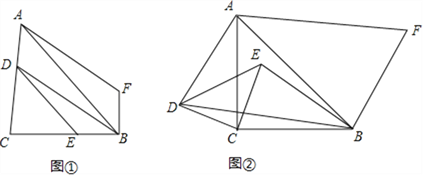
【题目】如图,△ABC与△DEC均为等腰直角三角形,∠ACB=∠DCE=90°,连接BE,将BE绕点B顺时针旋转90°,得BF,连接AD,BD,AF
(1)如图①,D、E分别在AC,BC边上,求证:四边形ADBF为平行四边形;
(2)△DEC绕点C逆时针旋转,其它条件不变,如图②,(1)的结论是否成立?说明理由.
(3)在图①中,将△DEC绕点C逆时针旋转一周,其它条件不变,问:旋转角为多少度时.四边形ADBF为菱形?直接写出旋转角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中, ![]() 厘米,
厘米, ![]() 厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.5厘米,每个铁环长4.6厘米,设铁环间处于最大限度的拉伸状态
(1)填表:
铁环个数 | 1 | 2 | 3 | 4 |
链条长(cm) | 4.6 | 8.2 | _____ | ____ |
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.17米长的链条,至少需要多少个铁环?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
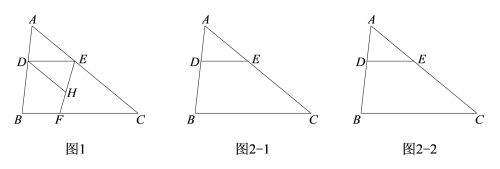
【题目】在三角形ABC中,点D在线段AB上,DE∥BC交AC于点E,点F在直线BC上,作直线EF,过点D作直线DH∥AC交直线EF于点H.
(1)在如图1所示的情况下,求证:∠HDE=∠C;
(2)若三角形ABC不变,D,E两点的位置也不变,点F在直线BC上运动.
①当点H在三角形ABC内部时,直接写出∠DHF与∠FEC的数量关系;
②当点H在三角形ABC外部时,①中结论是否依然成立?请在图2中画图探究,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com