练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．如图，将100张长为30cm、宽相等的长方形白纸，按如图所示的方法粘起来，粘合的部分宽为3cm，求粘合后总长度．

    分析 等量关系为：纸条总长度=30×纸条的张数-（纸条张数-1）×3，把相关数值代入即可求解．

    解答 解：每张纸条的宽度是30cm，x张应是30xcm，
    由图中可以看出4张纸条之间有3个粘合部分，那么x张纸条之间有（x-1）个粘合，应从总长度中减去．
    即：30x-（x-1）×3=27x+3，
    把x=100代入27x+3=2703
    答：总长度为2703厘米．

    点评 本题考查了列代数式的知识，找到纸条总长度和纸条张数的等量关系是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．在△ABC中，∠A=120°，若BC=12，则其外接圆O的直径为8$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）阅读理解：
    我们知道，只用直尺和圆规不能解决的三个经典的希腊问题之一是三等分任意角，但是这个任务可以借助如图所示的一边上有刻度的勾尺完成，勾尺的直角顶点为P，“宽臂”的宽度=PQ=QR=RS，（这个条件很重要哦！）勾尺的一边MN满足M，N，Q三点共线（所以PQ⊥MN）．
    下面以三等分∠ABC为例说明利用勾尺三等分锐角的过程：
    第一步：画直线DE使DE∥BC，且这两条平行线的距离等于PQ；
    第二步：移动勾尺到合适位置，使其顶点P落在DE上，使勾尺的MN边经过点B，同时让点R落在∠ABC的BA边上；
    第三步：标记此时点Q和点P所在位置，作射线BQ和射线BP．
    请完成第三步操作，图中∠ABC的三等分线是射线BQ、BP．
    （2）在（1）的条件下补全三等分∠ABC的主要证明过程：
    ∵PQ=QR，BQ⊥PR，
    ∴BP=BR．线段垂直平分线上的点到线段两个端点距离相等
    ∴∠RBQ=∠PBQ．
    ∵PQ⊥MN，PT⊥BC，PT=PQ，
    ∴∠PBQ=∠PBT．
    （角的内部到角的两边距离相等的点在角的平分线上）
    ∴∠RBQ=∠QBP=∠PBT．
    （3）在（1）的条件下探究：
    ∠ABS=$\frac{1}{3}$∠ABC是否成立？如果成立，请说明理由；如果不成立，请在下图中∠ABC的外部画出∠ABV=$\frac{1}{3}$∠ABC（无需写画法，保留画图痕迹即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．在边长为1的小正方形组成的网格中，把一个点先沿水平方向平移|a|格（当a为正数时，表示向右平移；当a为负数时，表示向左平移），再沿竖直方向平移|b|格（当b为正数时，表示向上平移；当b为负数时，表示向下平移），得到一个新的点，我们把这个过程记为（a，b），例如在图1中，从A到B记为：A→B（+1，+3）；从C到D记为：C→D（+1，-3）．
    请回答下列问题：
    （1）如图1，若点A的运动路线为：A→B→D→A，请计算点A运动过的总路程．
    （2）若点A运动的路线依次为：A→M（+2，+3），M→N（+1，-1），N→P（-2，+2），P→Q（+4，-4）．请你依次在图2上标出点M，N，P，Q的位置．
    （3）在图2中，若点A经过（m，n）得到点E，点E再经过（p，q）后得到Q，则m与p满足的数量关系是m+p=5；n与q满足的数量关系是n+q=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示，在△ABE和△ACD中，给出以下4个论断：
    （1）AB=AC；
    （2）AD=AE；
    （3）BE=CD；
    （4）∠DAM=∠EAN．
    以其中3个论断为题设，填入下面的“已知”栏中，1个论断为结论，填入下面的“求证”栏中，使之组成一个正确的命题，并写出证明过程．
    已知：AB=AC，AD=AE，BE=CD；
    求证：∠DAM=∠EAN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．新沟桥中学校园正在进行绿地改造，原有一正方形绿地，现将它每边都增加3米，面积增加了63平方米，问原绿地的边长为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．如图，△PQR是⊙O的内接正三角形，四边形ABCD是⊙O的内接正方形，且BC∥QR，则∠AOQ的度数为（　　）
    A．45°B．60°C．75°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列四个式子错误的是（　　）
    A．-3$\frac{5}{6}$$＜-3\frac{6}{7}$B．-1.38＞-1.384C．4.2＞-$\frac{21}{5}$D．-2＞-3

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图1，已知△ABC中，∠BAC=90°，AB=AC，AE是过A的一条直线，且BD⊥AE于点D，CE⊥AE于点E．
    （1）根据图1试证明：△ABD≌△CAE，并说明BD与DE，CE的关系：BD=DE=CE．
    （2 ）若直线AE绕A点旋转到图2位置时（BD＞CE），其余条件不变，试说明BD与DE，CE的关系又如何？（需把证明过程写出来）

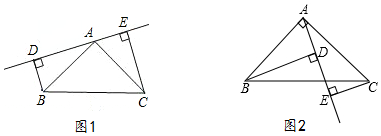
    查看答案和解析>>

    同步练习册答案