
【题目】如图,已知在正方形ABCD中、点E是BC边上一点,F为AB延长线上一点,且BE=BF,连接AE、EF、CF.
(1)若∠BAE=18°,求∠EFC的度数;
(2)求证:AE⊥CF.

【答案】(1)27°;(2)证明见解析.
【解析】
(1)依据△ABE≌△CBF,即可得出BAE=∠BCF=18°,再根据正方形ABCD中,∠ABC=90°,进而得出∠BEF=45°,即可得到∠EFC=∠BEF-∠BCF=45°-18°=27°;
(2)延长AE交CF于G,依据∠BCF+∠AFG=90°,∠BAE=∠BCF,即可得出∠AGF=90°,即AG⊥CF,进而得到AE⊥CF.
解:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠CBF=90°,
∵BE=BF,
∴△ABE≌△CBF(SAS),
∴∠BAE=∠BCF=18°,
又∵正方形ABCD中,∠ABC=90°,
∴∠BEF=∠BFE=45°,
∴∠EFC=∠BEF﹣∠BCF=45°﹣18°=27°;
(2)如图,延长AE交CF于G,
∵∠BCF+∠AFG=90°,∠BAE=∠BCF,
∴∠BAE+∠AFG=90°,
∴∠AGF=90°,即AG⊥CF,
∴AE⊥CF.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个.若销售单价每个降低2元,则每周可多卖出![]() 个.设销售价格每个降低
个.设销售价格每个降低![]() 元,每周销售量为y个.
元,每周销售量为y个.
(1)求出销售量![]() 个与降价
个与降价![]() 元之间的函数关系式;
元之间的函数关系式;
(2)设商户每周获得的利润为W元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
轴分别相交于点A(-1,0)和B(0,3),其顶点为D。
(1)求这条抛物线的解析式;
(2)画出此抛物线;
(3)若抛物线与![]() 轴的另一个交点为E,求△ODE的面积;
轴的另一个交点为E,求△ODE的面积;
(4)抛物线的对称轴上是否存在点P使得△PAB的周长最短。若存在请求出点P的坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)画出△ABC关于x轴对称的△A1B1C1,
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,
(3)△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴并写出对称轴;
(4)△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中任意抽取牛奶饮用,抽取任意一瓶都是等可能的.
(1)若小芳任意抽取1瓶,抽到过期的一瓶的概率是 ;
(2)若小芳任意抽取2瓶,请用画树状图或列表法求,抽出的2瓶牛奶中恰好抽到过期牛奶的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,动点P以
,动点P以![]() 的速度从A点出发,沿
的速度从A点出发,沿![]() 向C点移动,同时动点Q以
向C点移动,同时动点Q以![]() 的速度从点C出发,沿
的速度从点C出发,沿![]() 向点B移动,设P、Q两点移动的时间为t秒
向点B移动,设P、Q两点移动的时间为t秒![]() .
.

(1)t为多少时,以P、Q、C为顶点的三角形与![]() 相似?
相似?
(2)在P、Q两点移动过程中,四边形![]() 与
与![]() 的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
的面积能否相等?若能,求出此时t的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD为边BC上的中线,DE⊥AC于点E.
(1)请你写出图中所有与△CDE相似的三角形;
(2)若AB=10,BC=12,求EC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学在一次数学测验中解答的填空题,其中答对的是( )
A.若![]() ,则x=2B.若
,则x=2B.若![]() 的一个根是1,则k=2
的一个根是1,则k=2
C.若![]() ,则x=2D.若
,则x=2D.若![]() 的值为0,则x=1或2
的值为0,则x=1或2
查看答案和解析>>
科目:初中数学 来源: 题型:
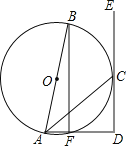
【题目】如图,AB是⊙O的直径,ED切⊙O于点C,AD交⊙O于点F,∠AC平分∠BAD,连接BF.
(1)求证:AD⊥ED;
(2)若CD=4,AF=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com