
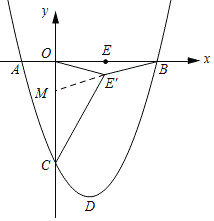
【题目】已知:如图1,抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,与y轴交于点C,点D为顶点.
两点,与y轴交于点C,点D为顶点.
![]() 求抛物线解析式及点D的坐标;
求抛物线解析式及点D的坐标;
![]() 若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有
若直线l过点D,P为直线l上的动点,当以A、B、P为顶点所作的直角三角形有![]() 且只有三个时,求直线l的解析式;
且只有三个时,求直线l的解析式;
![]() 如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到
如图2,E为OB的中点,将线段OE绕点O顺时针旋转得到![]() ,旋转角为
,旋转角为![]() ,连接
,连接![]() 、
、![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 与抛物线的交点坐标.
与抛物线的交点坐标.


【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】
![]() 由抛物线的交点式可知抛物线的解析式为
由抛物线的交点式可知抛物线的解析式为![]() ,通过整理可得到抛物线的解析式,然后利用配方法可得到抛物线的定点坐标;
,通过整理可得到抛物线的解析式,然后利用配方法可得到抛物线的定点坐标;
![]() 过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点
过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点![]() 以
以![]() 为直径的
为直径的![]() 如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点
如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点![]() 了,以AB为直径作
了,以AB为直径作![]() ,作QD与
,作QD与![]() 相切,则
相切,则![]() ,过
,过![]() 作
作![]() ,先求得点
,先求得点![]() 的坐标,于是可求得l的解析式,由图形的对称性可知点
的坐标,于是可求得l的解析式,由图形的对称性可知点![]() 的坐标还可以是
的坐标还可以是![]() ,然后可求得另一种情况;
,然后可求得另一种情况;
![]() 取
取![]() 使
使![]() ,连接
,连接![]() ,接下来,证明
,接下来,证明![]() ∽
∽![]() ,从而可得到
,从而可得到![]() ,故此当
,故此当![]() 、
、![]() 、
、![]() 在一条直线上时,
在一条直线上时,![]() 有最小值,最后,依据勾股定理求得
有最小值,最后,依据勾股定理求得![]() 的长度即可.
的长度即可.
![]() 抛物线
抛物线![]() 与x轴交于
与x轴交于![]() ,
,![]() 两点,
两点,
![]() .
.
![]() ,
,
![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() .
.
![]() 过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.
过点A、B分别作x轴的垂线,这两条垂线与直线l总是有交点的,即2个点Q.
以AB为直径的![]() 如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了.
如果与直线l相交,那么就有2个点Q;如果圆与直线l相切,就只有1个点Q了.
如图所示:以AB为直径作![]() ,作QD与
,作QD与![]() 相切,则
相切,则![]() ,过Q作
,过Q作![]() .
.

![]() ,
,![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
![]() 点Q的坐标为
点Q的坐标为![]() .
.
设l的解析式为![]() ,则
,则![]() ,解得:
,解得:![]() ,
,![]() ,
,
![]() 直线l的解析式为
直线l的解析式为![]() .
.
由图形的对称性可知:当直线l经过点![]() 时,直线l与
时,直线l与![]() 相切,
相切,
则![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 直线l的解析式为
直线l的解析式为![]() .
.
综上所述,直线l的解析式为![]() 或
或![]() .
.
![]() 如图所示:取M使
如图所示:取M使![]() ,连接
,连接![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
又![]() ,
,
![]() ∽
∽![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() 当M、
当M、![]() 、B在一条直线上时,
、B在一条直线上时,![]() 有最小值,
有最小值,
![]() 的最小值
的最小值![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某中学举办了绿色阅读节活动,为了表彰优秀,陈老师负责购买奖品,在购买时他发现身上所带的钱:若以2支钢笔和3个笔记本为一份奖品,则可买50份奖品;若以2支钢笔和6本笔记本为一份奖品,则可以买40份奖品,设钢笔单价为![]() 元/支,笔记本单价为
元/支,笔记本单价为![]() 元/支.
元/支.
(1)请用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)若用这笔钱全部购买笔记本,总共可以买几本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题发现
问题发现
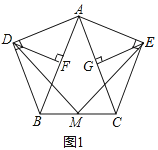
在等腰三角形ABC中,![]() ,分别以AB和AC为斜边,向
,分别以AB和AC为斜边,向![]() 的外侧作等腰直角三角形,如图1所示,其中
的外侧作等腰直角三角形,如图1所示,其中![]() 于点F,
于点F,![]() 于点G,M是BC的中点,连接MD和ME.
于点G,M是BC的中点,连接MD和ME.
填空:线段AF,AG,AB之间的数量关系是______;
线段MD,ME之间的数量关系是______.
![]() 拓展探究
拓展探究
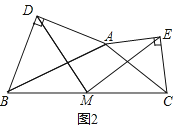
在任意三角形ABC中,分别以AB和AC为斜边向![]() 的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
的外侧作等腰直角三角形,如图2所示,M是BC的中点,连接MD和ME,则MD与ME具有怎样的数量关系和位置关系?并说明理由;
![]() 解决问题
解决问题
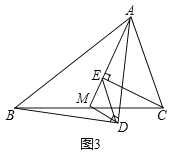
在任意三角形ABC中,分别以AB和AC为斜边,向![]() 的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若
的内侧作等腰直角三角形,如图3所示,M是BC的中点,连接MD和ME,若![]() ,请直接写出线段DE的长.
,请直接写出线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=6cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是6cm,则∠AOB的度数是( )

A.25°B.30°
C.60°D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系![]() 中
中![]() ,
,![]() ,
,![]() .
.

(1)作出![]() 关于直线
关于直线![]() 对称的图形△
对称的图形△![]() 并写出△
并写出△![]() 各顶点的坐标;
各顶点的坐标;
(2)将△![]() 向左平移2个单位,作出平移后的△
向左平移2个单位,作出平移后的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(3)观察![]() 和△
和△![]() ,它们是否关于某直线对称?若是,请指出对称轴,并求
,它们是否关于某直线对称?若是,请指出对称轴,并求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下表中的每一组值:
名称组别 |
|
|
| 名称组别 |
|
|
|
第1组 | 3 |
|
| 第5组 | |||
第2组 | 5 |
|
|
|
|
| |
第3组 | 7 |
|
|
|
|
| |
第4组 | 8 |
|
| 第 |
(1)根据表中前四组![]() 、
、![]() 、
、![]() 值的变化规律,第5组中
值的变化规律,第5组中![]() ;
;![]() ;第
;第![]() 组中
组中![]() ;
;![]() ;
;![]() .
.
(2)试证明以表中每组![]() 、
、![]() 、
、![]() 为边的三角形都是直角三角形.
为边的三角形都是直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算![]() 的近似值.
的近似值.
小明的方法:
∵![]() <
<![]() <
<![]() ,
,
设![]() =3+k(0<k<1).
=3+k(0<k<1).
∴![]() .
.
∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈![]() .
.
∴![]() ≈3+
≈3+![]() ≈3.67.
≈3.67.
问题:
(1)请你依照小明的方法,估算![]() 的近似值;
的近似值;
(2)请结合上述具体实例,概括出估算![]() 的公式:已知非负整数a、b、m,若a<
的公式:已知非负整数a、b、m,若a<![]() <a+1,且m=a2+b,则
<a+1,且m=a2+b,则![]() ≈ (用含a、b的代数式表示);
≈ (用含a、b的代数式表示);
(3)请用(2)中的结论估算![]() 的近似值.
的近似值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
(1)补全△A′B′C′
(2)画出AC边上的中线BD;
(3)画出AC边上的高线BE;
(4)求△ABD的面积 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com