
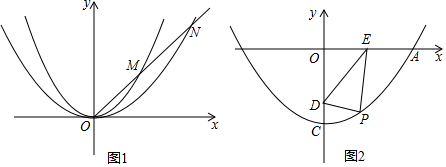
���� ��1�����㣨2��$\frac{1}{2}$������y=ax2���ɵõ����ۣ�
��2�����M��4k��4k2����N��8k��8k2�������������ľ��빫ʽ���ɵõ����ۣ�
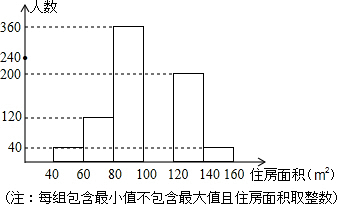
��3��������������������C3�Ľ���ʽΪy=$\frac{1}{8}$x2-8�����������ε������ʽ�õ����S=-$\frac{1}{4}$x2+3x+4 ��0��x��8 ����
������S=-$\frac{1}{4}$x2+3x+4=-$\frac{1}{4}$��x-6��2+13�����ǵõ���0��x��8 ��ȡֵ��Χ�ڣ�S��ȡֵΪ��4��S��13����S��ȡ4��13��10����������S=12ʱ��x������ֵ���Ӧ��������������P��λ��ʹS=12�����ǵõ����ۣ�
��� �⣺��1�����㣨2��$\frac{1}{2}$������y=ax2����ã�a=$\frac{1}{8}$��
��2��ֱ��y=kx��k��0���ֱ�һ�����ڵ�������C2��C1��M��N���㣬
�ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{8}{x}^{2}}\\{y=kx}\end{array}\right.$�ã�$\left\{\begin{array}{l}{{x}_{1}=4k}\\{{y}_{1}=4{k}^{2}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=0}\\{{y}_{2}=0}\end{array}\right.$���ⷽ����$\left\{\begin{array}{l}{y=\frac{1}{4}{x}^{2}}\\{y=kx}\end{array}\right.$�ã�$\left\{\begin{array}{l}{{x}_{3}=0}\\{{y}_{3}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{4}=8k}\\{{y}_{4}=8{k}^{2}}\end{array}\right.$��
��M��4k��4k2����N��8k��8k2����
��OM=$\sqrt{��4k��^{2}+��4{k}^{2}��^{2}}$=4k$\sqrt{{k}^{2}+1}$��MN=$\sqrt{��4k-8k��^{2}+��4{k}^{2}-8{k}^{2}��^{2}}$=4k$\sqrt{{k}^{2}+1}$��
��OM=MN��
��3��������������������C3�Ľ���ʽΪy=$\frac{1}{8}$x2-8��
��S=S��PDO+S��POE-S��ODE=3x+2����8-$\frac{1}{8}{x}^{2}$��-12
=-$\frac{1}{4}$x2+3x+4 ��0��x��8 ����
�ڡ�S=-$\frac{1}{4}$x2+3x+4=-$\frac{1}{4}$��x-6��2+13��
��0��x��8 ��ȡֵ��Χ�ڣ�S��ȡֵΪ��4��S��13��
��S��ȡ4��13��10��������
�ֵ�S=12ʱ��x������ֵ���Ӧ��������������P��λ��ʹS=12��
���Թ���11����PʹS��ֵΪ������
���� ���⿼���˴���ϵ���������Ľ���ʽ�������ľ��빫ʽ�������ε�����ļ��㣬���κ�������ֵ����ȷ�����������ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�д����������ڼ䣬ij��˾�Բμӱ��η�����������߽�����������ʾ����飬������1000�ݵ����ʾ�����ȫ���ջأ����ݵ����ʾ����������������������������Ƴɱ������£��������ߴ��㹺��ס����������������������Ƶ���ֲ�ֱ��ͼ��ͼ��
ij�д����������ڼ䣬ij��˾�Բμӱ��η�����������߽�����������ʾ����飬������1000�ݵ����ʾ�����ȫ���ջأ����ݵ����ʾ����������������������������Ƴɱ������£��������ߴ��㹺��ס����������������������Ƶ���ֲ�ֱ��ͼ��ͼ��| �����루��Ԫ�� | 1.2 | 1.8 | 3.0 | 5.0 | 10.0 |
| ������������������ˣ� | 200 | 300 | 400 | 70 | 30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
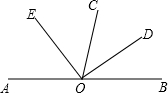 ��ͼ����O��ֱ��AB�ϣ�ODƽ�֡�BOC��OEƽ�֡�AOC����ͼ�л����Ľ���5�飮
��ͼ����O��ֱ��AB�ϣ�ODƽ�֡�BOC��OEƽ�֡�AOC����ͼ�л����Ľ���5�飮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
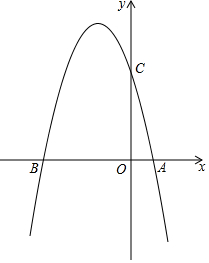 ��ͼ����֪�����߾���A��1��0����C��0��4�����㣬��x������һ��B����Գ�����x=-1.5��
��ͼ����֪�����߾���A��1��0����C��0��4�����㣬��x������һ��B����Գ�����x=-1.5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
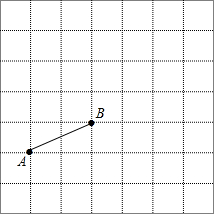 ��ͼ����֪A��-1��0����B��1��1�������߶�ABƽ�ƣ�ʹ��B���ڵ�D��3��4��������ʱ��A�ƶ�����C����
��ͼ����֪A��-1��0����B��1��1�������߶�ABƽ�ƣ�ʹ��B���ڵ�D��3��4��������ʱ��A�ƶ�����C�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
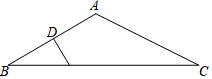 ��ͼ����ABC�У�AB=AC���ҡ�BAC=108�㣬��D��AB��һ���㣬����BC������һ��E��ʹ��B��D��EΪ��������������ABC���ƣ�
��ͼ����ABC�У�AB=AC���ҡ�BAC=108�㣬��D��AB��һ���㣬����BC������һ��E��ʹ��B��D��EΪ��������������ABC���ƣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ��������ı���չ��ͼ����ԭ���������롰���������ڵ�����Ե����ϱ�����ǣ�������
��ͼ��һ��������ı���չ��ͼ����ԭ���������롰���������ڵ�����Ե����ϱ�����ǣ�������| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com