
【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是梯形,AD∥BC,CA是∠BCD的平分线,且AB⊥AC,AB=4,AD=6,则tanB=( )
A.2![]()
B.2![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当△ABP≌△ADN时,BP=4 ![]() ﹣4.
﹣4.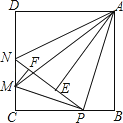
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B=45°,∠C=30°,点D是BC上一点,连接AD,过点A作AG⊥AD,在AG上取点F,连接DF.延长DA至E,使AE=AF,连接EG,DG,且GE=DF.
(1)若AB=2 ![]() ,求BC的长;
,求BC的长;
(2)如图1,当点G在AC上时,求证:BD= ![]() CG;
CG;
(3)如图2,当点G在AC的垂直平分线上时,直接写出 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,田亮同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( ) 
A.垂线段最短
B.经过一点有无数条直线
C.经过两点,有且仅有一条直线
D.两点之间,线段最短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,AQ=PQ,PR⊥AB于点R,PS⊥AC于点S,PR=PS,则下列结论:①点P在∠A的角平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别在边AB,BC上,且AE= ![]() AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号)
AB,将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是(填序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,D点在抛物线y= ![]() x2+bx+c上,且OB=OC,AB=5,tan∠ACB=
x2+bx+c上,且OB=OC,AB=5,tan∠ACB= ![]() ,M是抛物线与y轴的交点.
,M是抛物线与y轴的交点.
(1)求直线AC和抛物线的解析式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动.问:当P运动到何处时,△APQ是直角三角形?
(3)在(2)中当P运动到某处时,四边形PDCQ的面积最小,求此时△CMQ的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com