
【题目】如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3 ,且AC=12,则DE的长度是( )

A. 3B. 6C. ![]() D.
D. ![]()
【答案】D
【解析】
根据∠EDC:∠EDA=1:3,可得∠EDC=22.5°,∠EDA=67.5°,再由AC=12,求得DE.
解:∵四边形ABCD是矩形,
∴∠ADC=90°,AC=BD=12,OA=OC=![]() AC=6,OB=OD=
AC=6,OB=OD=![]() BD=6,
BD=6,
∴OC=OD,
∴∠ODC=∠OCD,
∵∠EDC:∠EDA=1:3,∠EDC+∠EDA=90°,
∴∠EDC=22.5°,∠EDA=67.5°,
∵DE⊥AC,
∴∠DEC=90°,
∴∠DCE=90°-∠EDC=67.5°,
∴∠ODC=∠OCD=67.5°,
∵∠ODC+∠OCD+∠DOC=180°,
∴∠COD=45°,
∴OE=DE,
∵OE2+DE2=OD2,
∴2DE2=OD2=36,
∴DE=![]() ,
,
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,A、B在数轴上对应的数分别用![]() 、
、![]() 表示,且
表示,且![]() .
.
(1)数轴上点A表示的数是 ,点B表示的数是
(2)若一动点P从点A出发,以3个单位长度/秒速度由A向B运动;动点Q从原点O出发,以1个单位长度/秒速度向B运动,点P、Q同时出发,点Q运动到B点时两点同时停止.设点Q运动时间为t秒.
①若P从A到B运动,则P点表示的数为 ,Q点表示的数为 .用含![]() 的式子表示)
的式子表示)
②当t为何值时,点P与点Q之间的距离为2个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() ,有下列说法:
,有下列说法:
①如果当x≤1时![]() 随
随![]() 的增大而减小,则m≥1;
的增大而减小,则m≥1;
②如果它的图象与x轴的两交点的距离是4,则![]() ;
;
③如果将它的图象向左平移3个单位后的函数的最小值是-4,则m=-1;
④如果当x=1时的函数值与x=2013时的函数值相等,则当x=2014时的函数值为-3.
其中正确的说法是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为庆祝建国七十周年,南岗区准备对某道路工程进行改造,若请甲工程队单独做此工程需4个月完成,若请乙工程队单独做此工程需6个月完成,若甲、乙两队合作2个月后,甲工程队到期撤离,则乙工程队再单独需几个月能完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
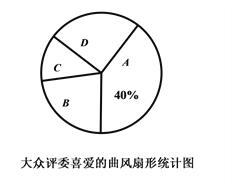
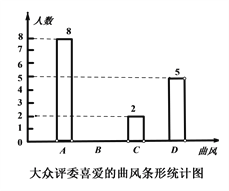
【题目】春雨初歇,绿意葱茏,重庆南开(融侨)中学初2020级举行了“春天的赞礼”为主题的合唱比赛,各班演唱歌曲的曲风有:青春舞曲、经典名曲、动漫神曲、励志金曲四种类型,为了了解同学们对各种曲风的喜爱程度。校学生处对大众评委喜爱的歌曲曲风进行了调查,(A—喜爱青春舞曲、B—喜爱经典名曲、C—喜爱动漫神曲、D—喜爱励志金曲),先根据调查得到如下图不完整的统计图,请结合图中信息完成下列问题:
![]() 扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
扇形统计图中“C—喜爱动漫神曲”对应扇形圆心角为【1】度,并补全条形统计图.
![]() 在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
在此次比赛中,甲班演唱的《四季问候》和乙班演唱的《东方之珠》获得一等奖,《司机问候》由2名男生和2名女生领唱,《东方之珠》由1名男生和2名女生领唱,校学生处打算分别从这两首歌曲的领唱中任意选取1名同学参加校合唱团,请用画树状图或列表的方法求出恰好选到1名男生和1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两实数a与b,M=![]() +
+![]() ,N=2ab
,N=2ab
(1)请判断M与N的大小,并说明理由。
(2)请根据(1)的结论,求![]() +
+![]() +3的最小值(其中x,y均为正数)
+3的最小值(其中x,y均为正数)
(3)请判断![]() +
+![]() +
+![]() abacbc的正负性(a,b,c为互不相等的实数)
abacbc的正负性(a,b,c为互不相等的实数)
(4)若n为正整数,则(n+1)(n+4)(n2+5n)+4的值为某一个整数的平方,试说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB、CD为两个建筑物,建筑物AB的高度为60米,从建筑物AB的顶点A点测得建筑物CD的顶点C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为45°.
(1)求两建筑物底部之间水平距离BD的长度;
(2)求建筑物CD的高度(结果保留根号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com