
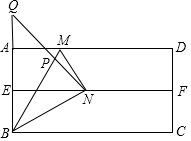
 如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3.
如图,四边形ABCD为矩形纸片,对折纸片,使得AD与BC重合,得到折痕EF,把纸片展平后,再把纸片沿着BM折叠,使得点A与EF上的点N重合,在折痕BM上取一点P,使得BP=BA,连接NP并延长.交BA的延长线于点Q.若AB=6.则AQ的长为3$\sqrt{3}$-3. 分析 根据折叠的性质得到AE=BE=$\frac{1}{2}$AB=3,BN=AB=6,据此可得∠BNE=30°,再根据BP=BA=BN,求得∠BNP=75°,∠ENQ=75°-30°=45°,再根据△QEN是等腰直角三角形,即可得到QE=NE=$\sqrt{3}$BE=3$\sqrt{3}$,进而得出AQ=QE-AE=3$\sqrt{3}$-3.
解答  解:由折叠可得,AE=BE=$\frac{1}{2}$AB=3,BN=AB=6,
解:由折叠可得,AE=BE=$\frac{1}{2}$AB=3,BN=AB=6,
∴∠BNE=30°,∠ABN=60°,
∴∠MBN=$\frac{1}{2}$∠ABN=30°,
∵BP=BA=BN,
∴△BNP中,∠BNP=$\frac{180°-30°}{2}$=75°,
∴∠ENQ=75°-30°=45°,
又∵EF⊥AB,
∴△QEN是等腰直角三角形,
∴QE=NE=$\sqrt{3}$BE=3$\sqrt{3}$,
∴AQ=QE-AE=3$\sqrt{3}$-3.
故答案为:3$\sqrt{3}$-3.
点评 本题主要考查了折叠问题以及等腰直角三角形的判定与性质的运用,解题时注意:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
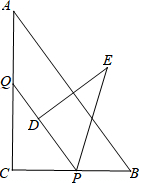 如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
如图,Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在BC、AC上,CP=3x,CQ=4x (0<x<1),把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com