练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，已知：OD为∠AOB的平分线，DC⊥OA，垂足为C，∠OAD十∠OBD＝180°．

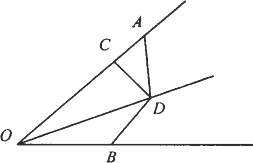
    (1)求证：AO＋BO＝2CO；

    (2)若将条件“∠OAD＋∠OBD＝180°”与结论“AO＋BO＝2CO”互换，结论还成立吗？请证明．

    答案：
    解析：

    　　(1)过D作DE⊥OB于E，先证明△DCA≌△DEB，可证得AO＋BO＝2CO;

    　　(2)过D作DE⊥OB于E，由AO＋BO＝2CO，可得AC＝BE，进一步证明△DCA≌△DEB，可得出∠OAD＋∠OBD＝180°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

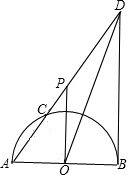    精英家教网如图，已知：AB为⊙O的直径，AB=6
    		3
    ，弧AC=
    1
    3
    弧AB，过B点的切线与AC的延长线交于点D．
    （1）求OD的长；
    （2）若P是AD上的任意一点（不与A、D重合），设PD=x，求△POD的面积y与x的函数关系式，并指出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•广安）如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图①：已知点C为线段AB上一点，且D、E分别是线段AB、BC的中点，
    （1）若AC=5cm，BC=4cm，试求线段DE的长度．
    （2）如果（1）中的BC=a，其他条件不变，试求DE的长度．
    （3）根据（1）（2）的计算结果，有关线段DE的长度你能得出什么结论？
    （4）如图②，已知∠AOC=α，∠BOC=β，且OD、OE分别为∠AOB、∠BOC的角平分线，请直接写出∠DOE度数的表达式．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（四川广安卷）数学（解析版） 题型：选择题

    （2013年四川广安3分）如图，已知半径OD与弦AB互相垂直，垂足为点C，若AB=8cm，CD=3cm，则圆O的半径为【    】

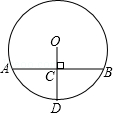
    A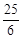．cm      B．5cm       C．4cm      D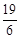．cm

     

    查看答案和解析>>

    同步练习册答案