
| k-2 | x |
科目:初中数学 来源: 题型:阅读理解
| AB |
| AB |
| AB |
| BA |
| OP |
| OP |
| OA |
| OA |
| 2 |
| OA |
| OB |
| 3 |
| MA |
| AP |
| MP |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 2 |
| 3 |

查看答案和解析>>
科目:初中数学 来源:2008-2009学年重庆市一中九年级(上)期末数学试卷(解析版) 题型:解答题
 .当P点运动时,求y与x的函数关系式并写出自变量x的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中y≥0的部分有何关系?
.当P点运动时,求y与x的函数关系式并写出自变量x的取值范围,在同一直角坐标系中,该函数的图象与图①的抛物线中y≥0的部分有何关系? (点M、N、G按逆时针顺序),当点G在抛物线上运动时,直线AM、GH是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由.
(点M、N、G按逆时针顺序),当点G在抛物线上运动时,直线AM、GH是否存在某种位置关系?若存在,写出并证明你的结论;若不存在,请说明理由. 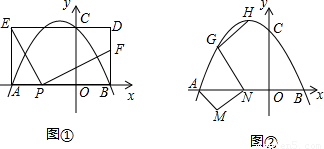
查看答案和解析>>
科目:初中数学 来源:第7章《锐角三角函数》中考题集(29):7.5 解直角三角形(解析版) 题型:解答题
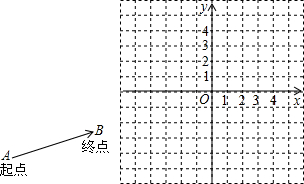
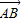 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|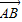 |.显然,有向线段
|.显然,有向线段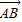 和有向线段
和有向线段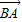 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.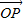 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|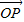 |=3.
|=3.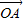 有向线段,使得
有向线段,使得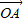 =3
=3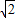 ,
,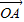 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;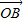 的终点B的坐标为(3,
的终点B的坐标为(3,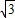 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;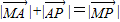 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)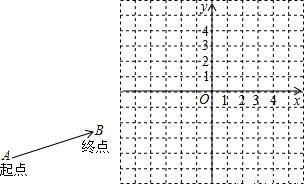
查看答案和解析>>
科目:初中数学 来源:第4章《锐角三角形》中考题集(26):4.3 解直角三角形及其应用(解析版) 题型:解答题
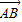 (起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|
(起点字母A写在前面,终点字母B写在后面).线段AB的长度叫做有向线AB的长度(或模),记为|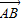 |.显然,有向线段
|.显然,有向线段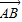 和有向线段
和有向线段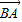 长度相同.方向不同,它们不是同一条有向线段.
长度相同.方向不同,它们不是同一条有向线段.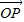 ,其方向与x轴正方向相同,长度(或模)是|
,其方向与x轴正方向相同,长度(或模)是|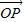 |=3.
|=3. 有向线段,使得
有向线段,使得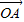 =3
=3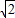 ,
,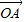 与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;
与x轴正半轴的夹角是45°,且与y轴的负半轴的夹角是45°;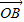 的终点B的坐标为(3,
的终点B的坐标为(3,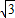 ),试求出它的模及它与x轴正半轴的夹角;
),试求出它的模及它与x轴正半轴的夹角;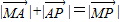 成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)
成立吗?试画出示意图加以说明.(示意图可以不画在平面直角坐标系中)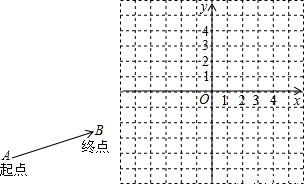
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com