
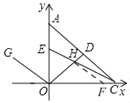
【题目】如图,以直角△AOC的直角顶点O为原点,以OC,OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足![]() .
.

(1)点A的坐标为________;点C的坐标为________.
(2)已知坐标轴上有两动点P,Q同时出发,P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动,点P到达O点整个运动随之结束.AC的中点D的坐标是(4,3),设运动时间为t秒.问:是否存在这样的t,使得△ODP与△ODQ的面积相等?若存在,请求出t的值;若不存在,请说明理由.
(3)在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且y轴平分∠GOD.点E是线段OA上一动点,连接接CE交OD于点H,当点E在线段OA上运动的过程中,探究∠GOA,∠OHC,∠ACE之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
【答案】(1)(0,6),(8,0);(2)存在t=2.4时,使得△ODP与△ODQ的面积相等;(3)2∠GOA+∠ACE=∠OHC,理由见解析.
【解析】
(1)根据算术平方根的非负性,绝对值的非负性即可求解;
(2)根据运动速度得到OQ=t,OP=8-2t,根据△ODP与△ODQ的面积相等列方程求解即可;
(3)由∠AOC=90°,y轴平分∠GOD证得OG∥AC,过点H作HF∥OG交x轴于F,得到∠FHC=∠ACE,∠FHO=∠GOD,从而∠GOD+∠ACE=∠FHO+∠FHC,即可证得2∠GOA+∠ACE=∠OHC.
(1)∵![]() ,
,
∴a-b+2=0,b-8=0,
∴a=6,b=8,
∴A(0,6),C(8,0);
故答案为:(0,6),(8,0);
(2)由(1)知,A(0,6),C(8,0),
∴OA=6,OB=8,
由运动知,OQ=t,PC=2t,
∴OP=8-2t,
∵D(4,3),
∴![]() ,
,
![]() ,
,
∵△ODP与△ODQ的面积相等,
∴2t=12-3t,
∴t=2.4,
∴存在t=2.4时,使得△ODP与△ODQ的面积相等;
(3)2∠GOA+∠ACE=∠OHC,理由如下:
∵x轴⊥y轴,
∴∠AOC=∠DOC+∠AOD=90°,
∴∠OAC+∠ACO=90°.
又∵∠DOC=∠DCO,
∴∠OAC=∠AOD.
∵x轴平分∠GOD,
∴∠GOA=∠AOD.
∴∠GOA=∠OAC.
∴OG∥AC,
如图,过点H作HF∥OG交x轴于F,
∴HF∥AC,
∴∠FHC=∠ACE.
∵OG∥FH,
∴∠GOD=∠FHO,
∴∠GOD+∠ACE=∠FHO+∠FHC,
即∠GOD+∠ACE=∠OHC,
∴2∠GOA+∠ACE=∠OHC.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】[x]表示不超过x的最大整数,例如[﹣3.5]=﹣4,[2.1]=2,若y=x﹣[x],下列命题:①当x=﹣0.5时,y=0.5;②y的取值范围是:0≤y≤1;③对于所有的自变量x,函数值y随着x增大而一直增大.其中正确命题有 (只填写正确命题的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴相交于C点.
(1)求m的值及C点坐标;
(2)在直线BC上方的抛物线上是否存在一点M,使得它与B,C两点构成的三角形面积最大,若存在,求出此时M点坐标;若不存在,请简要说明理由;
(3)P为抛物线上一点,它关于直线BC的对称点为Q.
①当四边形PBQC为菱形时,求点P的坐标;
②点P的横坐标为t(0<t<4),当t为何值时,四边形PBQC的面积最大,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A,B望灯塔C,测得∠NAC=30,∠NBC=60.

(1)求从海岛B到灯塔C的距离;
(2)这条船继续向正北航行,问在上午或下午的什么时间小船与灯塔C的距离最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
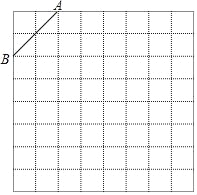
【题目】如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
(1)在网格中建立平面直角坐标系,使A点坐标为(﹣2,4),B点坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是 ;
(3)求△ABC中BC边上的高长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形MNPQ中,动点R从点N出发,沿着![]() 方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是( )
方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是( )

A.矩形MNPQ的周长是18B.当x=2时,y=5
C.当x=6时,y=10D.当y=8时,x=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解学生的课外学习负担,即墨区某中学数学兴趣小组决定对本校学生每天的课外学习情况进行调查,他们随机抽取本校部分学生进行了问卷调查,并将调查结果分为A,B,C,D四个等级,列表如下:
等级 | A | B | C | D |
每天课外学习时间 |
|
|
|
|
根据调查结果绘制了如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:

![]() 本次抽样调查共抽取了多少名学生?其中学习时间在B等级的学生有多少人?
本次抽样调查共抽取了多少名学生?其中学习时间在B等级的学生有多少人?
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 表示D等级的扇形圆心角的度数是多少?
表示D等级的扇形圆心角的度数是多少?
![]() 该校共有2000名学生,每天课外学习时间在2小时以内的学生有多少人?
该校共有2000名学生,每天课外学习时间在2小时以内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,a),B(b,a),且a,b满足(a﹣3)2+|b﹣6|=0,现同时将点A,B分别向下平移3个单位,再向左平移2个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD;
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=![]() S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
S四边形ABCD?若存在这样一点,求出点M的坐标,若不存在,试说明理由;
(3)点P是直线BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合),直接写出∠BAP,∠DOP,∠APO之间满足的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com