
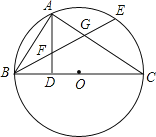
【题目】如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,弧AB=弧AE,BE分别交AD,AC于点F,G.
(1)求证:FA=FG;
(2)若BD=DO=2,求弧EC的长度.
【答案】(1)证明见解析;(2)![]() π.
π.
【解析】
(1)根据BC是⊙O的直径,AD⊥BC,弧AB=弧AE,推出∠AGB=∠CAD,即可推得FA=FG.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据弧AB=弧AE,求出∠EOC=60°,即可求出弧EC的长度是多少.
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°.
∴∠ABE+∠AGB=90°.
∵AD⊥BC,
∴∠C+∠CAD=90°.
∵![]() =
=![]() ,
,
∴∠C=∠ABE.
∴∠AGB=∠CAD.
∴FA=FG.
(2)连接AO,EO.
∵BD=DO=2,AD⊥BC,
∴AB=AO.
∵AO=BO,
∴AB=AO=BO.
∴△ABO是等边三角形.
∴∠AOB=60°.
∵![]() =
=![]() ,
,
∴∠AOE=60°.
∴∠EOC=60°.
∴![]() 的长为2π×(2+2)×
的长为2π×(2+2)×![]() =
=![]() π.
π.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】解下列方程:
(1)解方程::x2﹣6x﹣5=0; (2)解方程:2(x﹣1)2=3x﹣3;
(3)求抛物线![]() 的顶点坐标、对称轴和它与坐标轴的交点坐标.
的顶点坐标、对称轴和它与坐标轴的交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
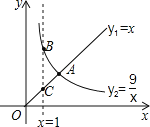
【题目】函数y1=x(x≥0),y2=![]() (x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当x<3时,y2>y1;③当x=1时,BC=8;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是( )
(x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当x<3时,y2>y1;③当x=1时,BC=8;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是( )
A. ①③④ B. ①②③④ C. ②③④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,BC的延长线于⊙O的切线AF交于点F.
(1)求证:∠ABC=2∠CAF;
(2)若AC=2![]() ,CE:EB=1:4,求CE的长.
,CE:EB=1:4,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
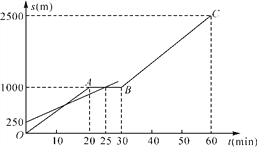
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500 m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(7分)某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).

(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市大力发展绿色交通,构建公共绿色交通体系,“共享单车”的投入使用给人们的出行带来便利.小明随机调查了若干市民租用共享单车的骑车时间t(单位:分),将获得的数据分成四组,绘制了如图统计图,请根据图中信息,解答下列问题:


(1)这次被调查的总人数是______;
(2)补全条形统计图;
(3)在扇形统计图中,求表示A组(t≤10分)的扇形圆心角的度数;
(4)如果骑共享单车的平均速度为12km/h,请估算,在租用共享单车的市民中,骑车路程不超过6km的人数所占的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有______人.
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人捐款5元,初中生每人捐款10元,高中生每人捐款15元,大学生每人捐款20元,平均每人捐款多少元?
(3)在(2)的条件下,把每个学生的捐款数(以元为单位)一一记录下来,则在这组数据中,众数和中位数分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com