
【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.

【答案】(1)见解析;(2)105°
【解析】试题分析:(1)根据正方形的性质可得BC=CD,∠ECB=∠ECD=45°,利用全等三角形的判定方法判定△BEC≌△DEC,(2)根据全等三角形的性质可得∠BEC=∠DEC= ![]() ,因为∠BED=120°,所以∠BEC=60°=∠AEF,
,因为∠BED=120°,所以∠BEC=60°=∠AEF,
所以∠EFD=60°+45°=105°.
试题解析: (1)证明:∵四边形ABCD是正方形,∴BC=CD,∠ECB=∠ECD=45°,
∴在△BEC与△DEC中,
 ,
,
∴△BEC≌△DEC(SAS),
(2)∵△BEC≌△DEC,
∴∠BEC=∠DEC= ![]() ,
,
∵∠BED=120°,
∴∠BEC=60°=∠AEF,
∴∠EFD=60°+45°=105°.


科目:初中数学 来源: 题型:
【题目】将一列有理数-1,2,-3,4,-5,6,…如图排序,根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么“峰4”中C的位置是有理数________,有理数“2018”应排在A,B,C,D,E中的________位置.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点 A 表示的有理数为﹣4,点 B 表示的有理数为 6,点 P 从 点 A 出发以每秒 2 个单位长度的速度在数轴上沿由 A 到 B 方向运动,当点 P 到 达点 B 后立即返回,仍然以每秒 2 个单位长度的速度运动至点 A 停止运动.设 运动时间为 t(单位:秒).
(1)求 t=2 时点 P 表示的有理数;
(2)求点 P 是 AB 的中点时 t 的值;
(3)在点 P 由点 A 到点 B 的运动过程中,求点 P 与点 A 的距离(用含 t 的代数式表示);
(4)在点 P 由点 B 到点 A 的返回过程中,点 P 表示的有理数是多少(用含 t 的 代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于![]() 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=2 ![]() ,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将
,以点C为圆心,CB的长为半径画弧,与AB边交于点D,将 ![]() 绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为
绕点D旋转180°后点B与点A恰好重合,则图中阴影部分的面积为 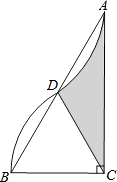
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD对角线AC上一点,EF⊥AB,EG⊥BC,垂足分别为F,G,若正方形ABCD的周长是40cm.
(1)求证:四边形BFEG是矩形;
(2)求四边形EFBG的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,直线
,直线![]() ,垂足为O,直线PQ经过点O,且
,垂足为O,直线PQ经过点O,且![]() 点B在直线l上,位于点O下方,
点B在直线l上,位于点O下方,![]() 点C在直线PQ上运动
点C在直线PQ上运动![]() 连接BC过点C作
连接BC过点C作![]() ,交直线MN于点A,连接
,交直线MN于点A,连接![]() 点A、C与点O都不重合
点A、C与点O都不重合![]() .
.
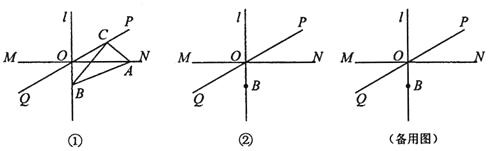
![]() 小明经过画图、度量发现:在
小明经过画图、度量发现:在![]() 中,始终有一个角与
中,始终有一个角与![]() 相等,这个角是________________;
相等,这个角是________________;
![]() 当
当![]() 时,在图
时,在图![]() 中画出示意图并证明
中画出示意图并证明![]() ;
;
![]() 探索
探索![]() 和
和![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com