
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
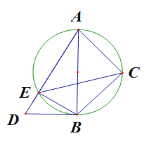
(1)求证:EC平分∠AEB;
(2)求![]() 的值.
的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;
(2)设AB与CE交于点M.根据角平分线的性质得出![]() .易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=
.易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=![]() BE,那么
BE,那么![]() .作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出
.作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出![]() ,进而求出
,进而求出
(1)证明:∵Rt△ACB中,∠ACB=90°,∠ABC=45°,
∴∠BAC=∠ABC=45°,
∵∠AEC=∠ABC,∠BEC=∠BAC,
∴∠AEC=∠BEC,
即EC平分∠AEB;
(2)如图,设AB与CE交于点M.

∵EC平分∠AEB,
∴![]() .
.
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE=![]() ,
,
∴AE=![]() BE,
BE,
∴![]() .
.
作AF⊥CE于F,BG⊥CE于G.
在△AFM与△BGM中,
∵∠AFM=∠BGM=90°,∠AMF=∠BMG,
∴△AFM∽△BGM,
∴![]() ,
,
∴ .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(a>0)的图象与x轴交于A、B两点,(A在B左侧,且OA<OB),与y轴交于点C.
(1)求C点坐标,并判断b的正负性;
(2)设这个二次函数的图像的对称轴与直线AC交于点D,已知DC:CA=1:2,直线BD与y轴交于点E,连接BC,
①若△BCE的面积为8,求二次函数的解析式;
②若△BCD为锐角三角形,请直接写出OA的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】潮州旅游文化节开幕前,某凤凰茶叶公司预测今年凤凰茶叶能够畅销,就用32000元购进了一批凤凰茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批凤凰茶叶,所购数量是第一批购进数量的2倍,但每千克凤凰茶叶进价多了10元.
(1)该凤凰茶叶公司两次共购进这种凤凰茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河西王府井销售一种 T 恤衫,每件进价为 40 元,经过市场调查,一周的销售量y 件与销售单价 x 元/件满足某种函数关系:
销售单价 x (元/件) | 50 | 60 | 70 | 80 | ||
一周的销售量 y(件) | 350 | 300 | 250 | 200 |
(1)请根据所学的知识,选择合适的函数模型,求出 y 与 x 的之间的函数关系式;
(2)设一周的销售利润为 w 元,请求出 w 与 x 的函数关系式,并确定当销售单价为多少时一周的销售利润最大,并求出最大利润;
(3)商场决定将一周销售 T 恤衫的利润全部捐给某村用于精准扶贫的水网改造项目,在商场购进该T 恤衫的资金不超过 6000 元情况下,请求出该商场最大捐款数额是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
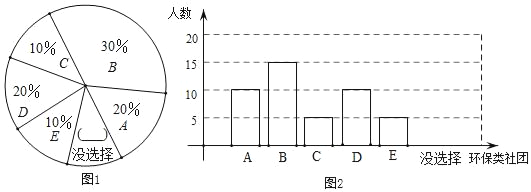
【题目】某校创建“环保示范学校”,为了解全校学生参加环保类杜团的意愿,在全校随机抽取了50名学生进行问卷调查,问卷给出了五个社团供学生选择(学生可根据自己的爱好选择一个社团,也可以不选),对选择了社团的学生的问卷情况进行了统计,如表:
社团名称 | A.酵素制作社团 | B.回收材料小制作社团 | C.垃圾分类社团 | D.环保义工社团 | E.绿植养护社团 |
人数 | 10 | 15 | 5 | 10 | 5 |
(1)填空:在统计表中,这5个数的中位数是 ;
(2)根据以上信息,补全扇形图(图1)和条形图(图2);
(3)该校有1400名学生,根据调查统计情况,请估计全校有多少学生愿意参加环保义工社团;
(4)若小诗和小雨两名同学在酵素制作社团或绿植养护社团中任意选择一个参加,请用树状图或列表法求出这两名同学同时选择绿植养护社团的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫:平均每天可售出20件,每件盈利40元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经市场调查发现:如果每件衬衫降价1元,那么平均每天就可多售出2件.若商场想平均每天盈利达1200元,那么每件衬衫应降价多少元?你若是商场经理,为获得最大利润,每件衬衫应降价多少元,此时最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个同学做了一个数字游戏:有三张正面写有数字-1,0,1的卡片片它们背面完全相同,将这三张卡片背面朝上洗匀后,其中一个同学随机抽取一张,将其正面的数字作为p的值,然后将卡片放回洗匀,另一个同学再从这三张卡片中随机抽取一张,将其正面的数字作为q的值,两次结果记为(p,q)
(1)请用树状图或列表法表示(p,q)所有可能出现的结果;
(2)求满足关于x的方程x2+px+q=0没有实数根的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com